





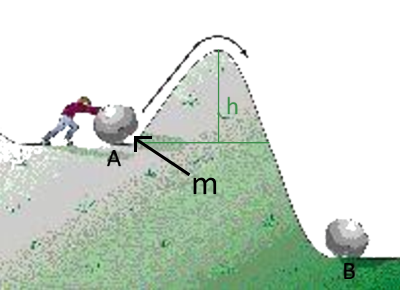
Reminder of physics: To push the ball of mass m from $A$ to $B$, Paul must produce work $W=9,8\;m\;h$ $m$ in $kg$ $h$ in meters $W$ in Joule One could say that this work is the activation energy of the transformation $A \longrightarrow B $ If Paul does not have that energy, the ball returns to $A$ !
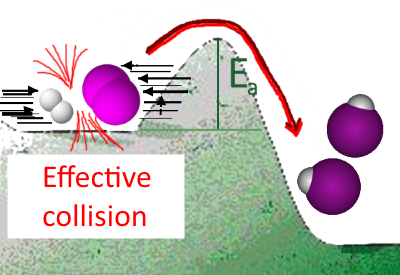
If the speed of the reactants is sufficient (temperature high enough), they can overcome their collision barrier constituted by the repulsion of the nuclei (activation energy) and turn into products

If the speed of the reactants is insufficient (too high temperature) or if the activation energy is too high, this is no longer possible!

Svante Arrhenius (1859-1929)
Arrhenius found that the rate constant can be expressed as follows:
$k=Ae^{-\frac{E_a}{R\cdot T}}$
where - $T$ is the absolute temperature (in $K$) - $E_a$ the activation energy (in $J$ ) - $R$ the ideal gas constant $(8.3 \frac{J}{mol\; K} )$ - A $\approx$ a constant for a given reaction It is seen that $k$ (and therefore the reaction rate) decreases when - $E_a$ increases (higher barrier!) - $T$ decreases (less collisions and weaker collisions)