





Inspired by the excellent → presentation of professor Tuckerman
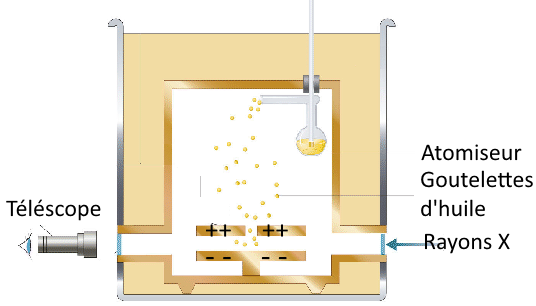
Droplets of oil with mass $M$ falling in an electric field $E$. Some remain suspended between the plates. These are (probably) those who captured an electron by action of X-rays. They have so the negative elementary charge $e$ Their weight must be equal to the electric force that holds them! We have: $M\cdot g$ $=$ $e\cdot E$ $\frac{M}{e}$ $=$ $\frac{g}{E}$ (1)
If $y$ is function of $x$, the differential equation $\frac{dy}{dx}$ $=$ $ay$ $+$ $b$ has one solution: $y$ $=$ $e^{ax}$ $-$ $\frac{b}{a}$ (2) Verification: $\frac{dy}{dx}$ = $ae^{ax}$ = $a(y$ $+$ $\frac{b}{a})$ = $ay$ $+$ $b$
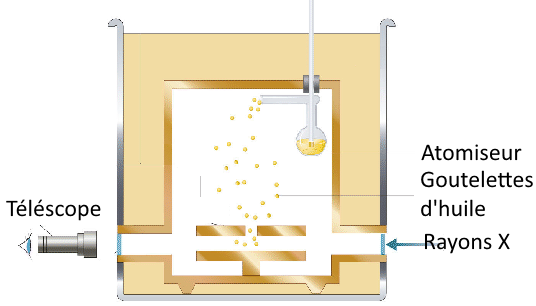
Now the oil droplets fall without electric field. In that case two forces act on them: 1) the weight $P$ = $M\cdot g$ 2) the friction force $F$ $ = $ $\gamma \cdot v $ where $\gamma $ is the friction coefficient, The resultant force is: $P$ $-$ $F$ $=$ $M\cdot g$ $-$ $\gamma \cdot v$ According to Newton's law, we have: $M\cdot \frac{dv}{dt}$ $=$ $M\cdot g$ $-$ $\gamma \cdot v$ $ \frac{dv}{dt}$ $=$ $g$ $-$ $\frac{\gamma}{M} \cdot v$ which is a differential equation of type (2) with $a$ $=$ $-\frac{\gamma}{M} $ and $b$ $=$ $g$ and therefore has the solution: $v$ $=$ $\frac{Mg}{\gamma}(1+e^{-\frac{\gamma \cdot t}{M}})$ As $\gamma $ is sufficiently large and $M$ small, the second term tends quickly to 0 and for the so stationary observed velocity $V$ we have: $V$ $=$ $\frac{Mg}{\gamma}$ (3) This equation makes it possible to determine $M$ and by (1) also $e $! Found:
$e$ $=$ $1,6\cdot 10^{-19}\;C$