





Inspired by the excellent → presentation of professor Tuckerman

$e$ is the charge of one electron. $m$ is the mass of one electron. $v$ is the speed in the x direction:

The electric field $E$ applies to the electron a force $F_E$ $=$ $e\cdot E$ This force causes a deflection in the vertical plane. The magnetic field $H$ applies to the electron a force $F_H$ $=$ $e\cdot v\cdot H$ This force causes also a deflection in the vertical plane.
We want to determinate the ratio $\frac{e}{m}$ :
In the x direction the electron velocity is constant. In fact, out of the hole of the anode, there is no force acting on it (Newton !). Let's get the fields so that the two forces exactly balance. Then the cathode rays are strictly horizontal:
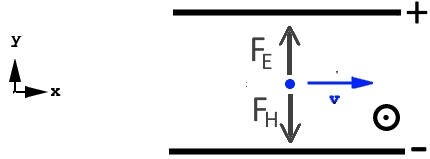
So: $F_E$ $=$ $F_H$ $eE$ $=$ $evH$ (1) $v$ $=$ $\frac{E}{H}$ Which determines the constant horizontal velocity $v$ !
Now let's only apply the electric field:
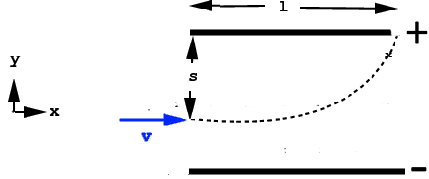
Over a horizontal distance $l$, the electron will be deflected by a vertical distance $s$ by the force $F_E$ . Let $T$ be the time required to travel both the horizontal distance $l$ and the vertical distance $s$ We find (uniform motion at a constant speed $v$ along the x axis): (2) $T$ = $\frac{l}{v}$ = $\frac{lH}{E}$ see (1) The acceleration alond axis y is: $a = \frac{F_E}{m}$ (Newton) so (uniformly accelerated motion): (3) $s$ = $\frac{1}{2}aT^2$ = $\frac{F_ET^2}{m}$ = $\frac{eET^2}{m}$ = $\frac{eE}{2m}(\frac{lH}{E})^2$ see (2) The equation $s$ $=$ $\frac{eE}{2m}(\frac{lH}{E})^2$ $\frac{e}{m}$ $=$ $\frac{2sE}{l^2H^2}$ allows to calculate the ratio $\frac{e}{m}$, since everything else is known or measurable. We find:
$\frac{e}{m}$ $=$ $1,76\cdot 10^{11} \frac{C}{kg}$