





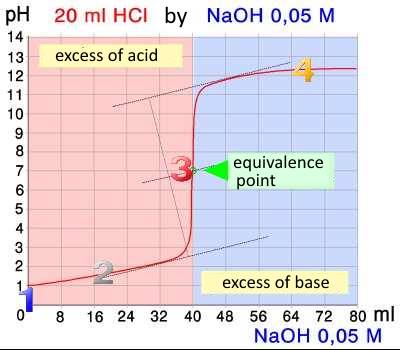
Thereafter we call $x$ the volume $(mL)$ of $NaOH$ already added.
$c_{Α}$ = $\frac{c_BV_B}{V_{Α}}$ = $\frac{0.05\cdot 0.040}{0.020}$ = $0.10 \frac{mol}{L}$
1.
The strong acid $HCl$ is present alone, its concentration is $c_{Α}=0,10 \;M$ $pH=-logc_{Α}$ $pH\;=\;1$
2.
(For simplicity, we consider the substances first as if they were not dissociated)

$c_{HCl}$ = $\frac{n_{HCl}}{(V_{Α}+x)10^{-3}}$ = $\frac{0.1\cdot20\cdot10^{-3}-0,05\cdot x\cdot10^{-3}}{(20+x)10^{-3}}$ = $\frac{2-0.05\cdot x}{20+x}$ $pH$ $ =$ $ -log( \frac{2-0,05\cdot x}{20+x})$
3.
$HCl$ and $NaOH$ reacted completely, remains a neutral $NaCl$ solution: $pH = 7$
4.

$c_{NaOH}$ = $\frac{n_{NaOH}}{(V_{Α}+x)10^{-3}}$ = $\frac{0.05\cdot x\cdot10^{-3}-0.1\cdot20\cdot10^{-3}}{(20+x)10^{-3}}$ = $\frac{0.05\cdot x-2}{20+x}$ $pH$ $ =$ $ 14$ $+$ $log( \frac{0.05\cdot x-2}{20+x})$
→ Here you find simulations of such titrations