






Pipette and burette were previously rinsed with the solutions that will be introduced later.
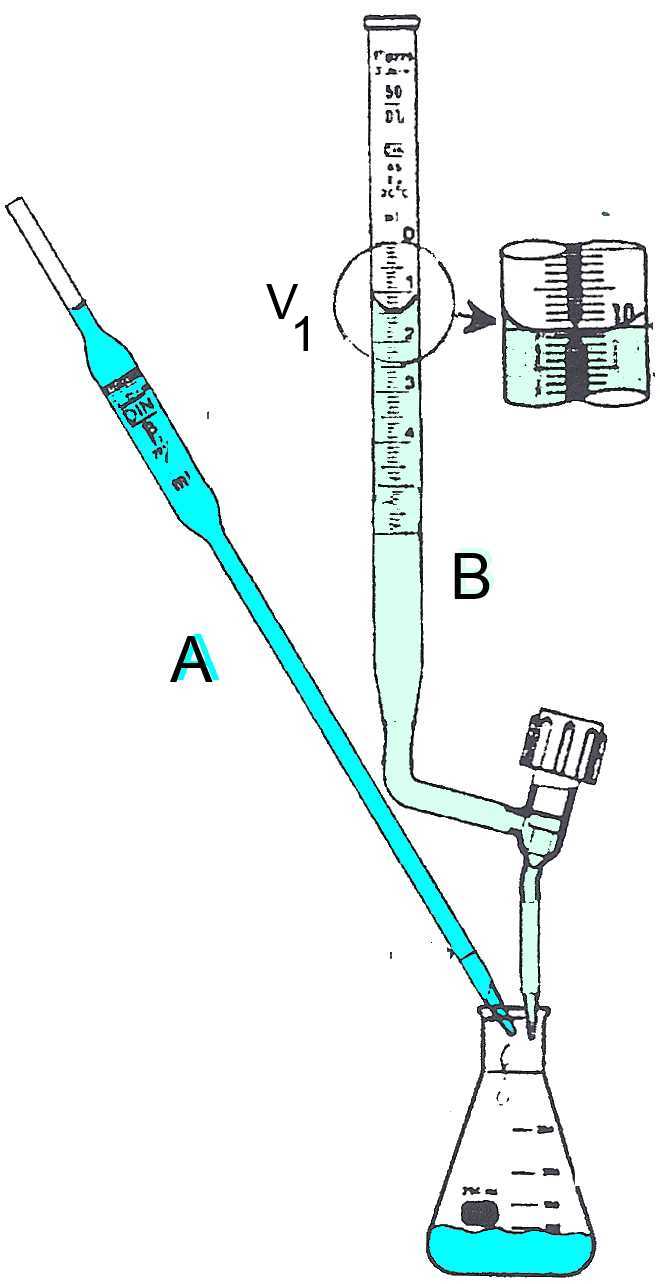
A: Acid or base concentration to be determined. Volume $V_{Α}$ is measured using the pipette. B: Base or acid of known concentration.
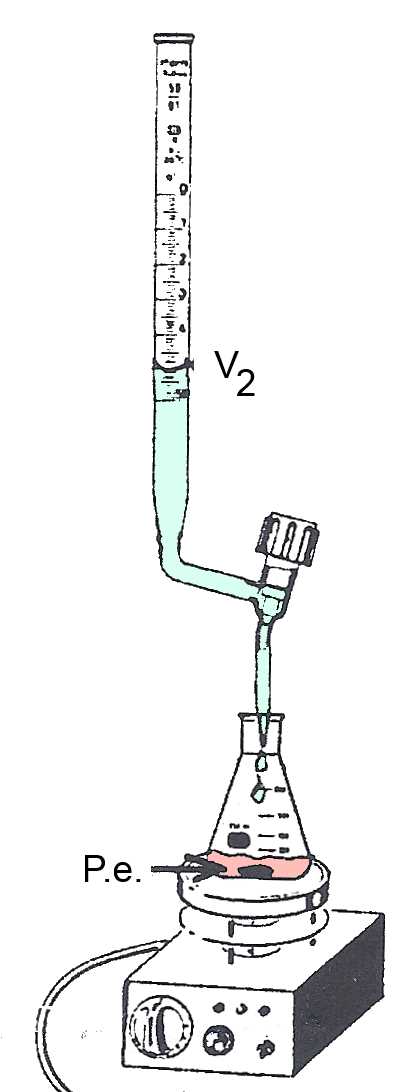
P.e. : At the equivalent point $Α$ has completely neutralized $B$. The P.e. is detected by the color change of an indicator or by the pHmeter. The volume of $B$ added up to the P.e. is $V_B$ $ = $ $V_2-V_1$
In P.e .: The number of moles of added B is equal to the number of moles present before A added B. $n_{Α} = n_B$ $c$Α$V_{Α}=c_BV_B$
In P.e .: $c_{Α}$ $=$ $\frac{c_BV_B}{V_{Α}}$
Example: $20 \;mL$ of a $HCl$ solution of unknown concentration $c_{Α}$ accurately measured using the pipette, are introduced into the Erlenmeyer flask. A drop of bromothymol is added. The solution becomes yellow. A solution of $0,10\frac{mol}{L}$ $NaOH$ is introduced in the burette. We measure $V_1 = 10.5 mL $. At the P.e. the solution turns blue. We measure $V_2 = 25.5 mL $. So we find: $c_{Α}$ $ =$ $\frac{c_BV_B}{V_{Α}}$ $=$ $\frac{0.10\cdot(0.0255-0.0105)}{0.020}$ $= $ $0.075 \frac{mol}{L}$