By its dissociation,
$HB$ $+$ $H_2O$ $\rightleftarrows$ $ H_3O^+$ $+$ $B$
an acid, however small, usually brings a lot more hydrogen ions in water that autoprotolysis of water itself.
Let's call ${HB}$ the number of moles of $HB$ introduced into the water before it is dissociated.
If $V$ is the final volume, the initial (formal) molarity is written:
$c_{HB}$ $=$ $\frac{n_{HB}}{V}$
Let's call $x$ the number of moles of hydronium $H_3O^+$ present in the solution when the dissociation equilibrium is achieved.
Then:
$H_3O^+$ $=$ $ \frac{x}{V}$
and
$pH$ $ =$ $ -log(\frac{x}{V})$
Let's calculate $x$:
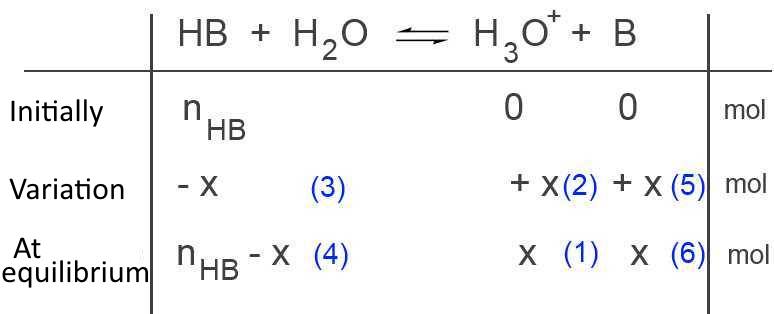We find in order:
(1) $x$ moles $H_3O^+$ at equilibrium
(2) $x$ moles $H_3O^+$ prodiuced
(3) $x$ moles $HB$ disappeared
(4) $n_{HB}-x$ moles $HB$ at equilibrium
(5) $x$ moles $B$ prodiuced
(6) $x$ moles $B$ at equilibrium
The molarities are at equilibrium:
$[H_3O^+]$ $=$ $\frac{x}{V}$
$[HB]$ $=$ $\frac{n_{HB}-x}{V}$
$[B]$ $=$ $\frac{x}{V}$
Introducing in the expression of the acidity constant $K_a$:
$K_a$ $=$ $\frac{[H_3O^+][B]}{[HB]}$ =
$\frac{\frac{x}{V}\frac{x}{V}}{\frac{n_{HB}-x}{V}}$ =
$\frac{\frac{x}{V}\frac{x}{V}}{\frac{n_{HB}}{V}-\frac{x}{V}}$ =
$\frac{[H_3O^+]^2}{c_{HB}-[H_3O^+]}$
$[H_3O^+]^2$ $+$ $K_a[H_3O^+]$ $-$ $K_ac_{HB}$ $=$ $0$
So, posing $y=[H_3O^+]$:
To determine the $pH$ of a diluted solution of weak acid, - we calculate a reasonable solution of the equation: $y^2$ $+$ $K_a\cdot y$ $-$ $K_a c_{HB}$ $=$ $0$ - we calculate $pH$ $=$ $-log\;y$
Example: Given a weak acid solution $0.10\frac{mol}{L}$ with $K_a$ $=$ $4.00\cdot 10^{-2}$: The equation $y^2$ $+$ $4.0\cdot10^{-2}\cdot y$ $-$ $4.0\cdot10^{-2}\cdot0.10$ $=$ $0$ provides the positive root: $y$ $=$ $8.3\cdot10^{-3}$ and so: $pH$ $=$ $-log\; y $ $=$ $2.1 $