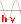
Bohr's theory has fully calculated the energy levels in H, but unfortunately it does not apply to more complex atoms! Something different had to be found while keeping the basic idea of the nature corpuscular and wave nature of light.
Albert Einstein found that there is no fundamental difference between matter and energy: A mass m of material and an amount of energy E can be converted mutually into one another according to the formula:
$E$ $=$ $m\cdot c^2$ (1) where $ c$ $=$ $3\cdot10^8\frac {m}{s}$ is the speed of light and $E$ the energy expressed in Joule.
Thus, $1\; kg$ of material can theoretically be converted into a tremendous amount of energy of $1\;(3\cdot 10^8)^2$ = $9\cdot10^{16}\; J$. This explains why, in atomic bombs, a lot of energy can be released from little matter!
A photon carrying an energy $E$ $=$ $h\nu$ acts (for example during a collision) as if it had a mass of: $m$ $=$ $\frac{E}{c^2}$ $=$ $\frac{h\nu}{c ^ 2}$ (2) $m$ is called the "rest mass" of the photon. This explains for example why it is perfectly possible to convert $\gamma $ photons to electrons and positrons (particles of the same mass as the electron, but with a positive charge)
Throwing common sense completely overboard, Louis de Broglie presented a bold hypothesis: Since photons behave sometimes like particles (shocks), sometimes as waves (diffraction), why not consider that all particles could do the same? Specifically, de Broglie was interested in a quantity which physicists know to be conserved in elastic collisions: Momentum: $p$ $=$ $mass \;\cdot\;speed $ . According to formula (2) the momentum of the photon is related to its wavelength: $p_{photon}$ $=$ $mc$ $=$ $\frac{h\nu}{c}$ $=$ $\frac{h}{\lambda}$ (3) De Broglie envisioned that the momentum of any particle of mass $m$ and evolving with speed $v$ is linked to the wavelength of the particle (!!!):
$p_ {particle}$ $=$ $m\cdot v$ $=$ $\frac{h}{\lambda}\;(4)$ where $m$ is the mass in kg of the particle and $\lambda $ the wavelength in meters.
Thus, an electron of mass $ m$ $ = $ $9.11\cdot10^{-31} kg$ moving with speed $v$ $=$ $10 ^ 6\frac{m}{s}$ behaves also as a wave of wavelength $\lambda$ $=$ $\frac {h} {mv}$ $ = $ $\frac {6.626\cdot10^{- 34}} {9.11\cdot10^{-31}\cdot10^6}$ $ = $ $ 7.27\cdot10^{-10}\; m$
De Broglie was right:
- Electrons may cause interferences like waves !
- A single electron projected onto a wall with two slits passes through the two slits (as a wave!)
Erwin Schrödinger pondered the mysterious condition of Bohr leading in a providential way to exact matches:
$mvr$ $=$ $\frac{nh}{2\pi}\;(5)$
where $ m $ is the mass of the electron, $v$ its speed on the $n^{th}$ circular orbit of the hydrogen atom and $r$ the radius of the orbit
Schrödinger tried to combine this condition with the ideas of de Broglie:
If $\lambda $ is the wavelength of the electron, we would have according to de Broglie:
$mv$ $=$ $\frac{h}{\lambda}\;(4)$
By combining (4) and (5), we find:
$2\pi r$ $ =$ $ n\cdot\lambda \;(6)$
where $ 2\pi r$ is the circumference of the orbit of the electron and $\lambda $ the wavelength!
The equation of Bohr means nothing other than that the wavelength of the electron should be contained an integer times in its orbit!
Such conditions are well known, for example in acoustics.
(Wavelength = the integer number of times contained in the length of the flute!)
The electrons of atoms obey resonance conditions.