Heat produces two major effects on the matter which receives or gives up heat : - a variation of temperature, or - a variation of physical state (solid, liquid, gaseous) of the matter
.Conduction" is the transfer of heat in solid matter. Metals have a better thermal conductivity than non-metals. (Example: The metal spoon in the hot coffee)
"Thermal radiation" is the transfer of heat by infrared rays (Part of the electromagnetic spectrum corresponding to radiation of a greater wavelength than visible light and smaller than microwave). All bodies, provided their temperature Kelvin is not zero, emit thermal radiation. (Example: An oven)
Heat causes migration of molecules in a liquid, generally from bottom to top because warm liquids are less dense than cold ones. (Example: Central warm water heating)
You need two times the quantity of heat to have a twofold rise in temperature:
The amount of heat is proportional to the elevation of temperature.
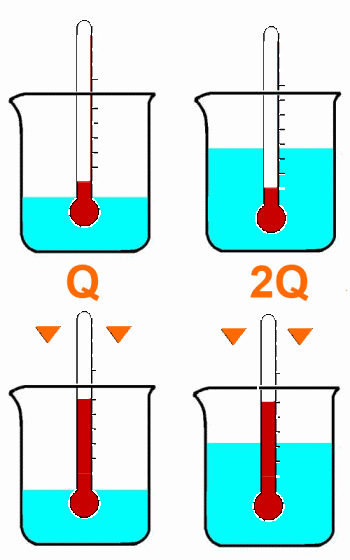You need two times the amount of heat to produce the same rise of temperature of a double mass:
The amount of heat is proportional to the mass.
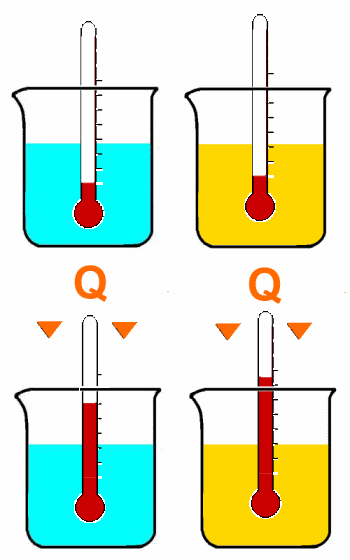Heating different matters, a different result is obtained with the same amount of heat:
The amount of heat depends on the matter.
$\Delta\; Q$ $ =$ $ c\;m\;\Delta\; T$ $\Delta\; Q$ : received heat $\Delta\; T$ : variation of temperature $m$ : mass $c$ : specific heat capacity (constant) depending on the matter.
The calorie is the amount of heat which rises the temperature of $1 \;g$ water by $1^oC$.
Introducing this definition in the fundamental formula, it follows : $\Delta\; Q$ $ =$ $ c\;m\;\Delta\; T$ $1\;cal$ $=$ $ c\dot 1\;g\cdot 1\;K$ $c$ $=$ $\frac{1\;cal }{1g\;1K}$ $c$ $=$ $1 \frac{cal}{g \cdot K}$
$c_{H_2O}$ $=$ $1 \;\frac{cal}{g \cdot K}$
A lump of sugar has a mass of $3\; g$. The combustion of $1\; g$ of sugar liberates $4\; kcal$. How many lumps must theoretically be burnt to heat $600\; g$ coffee (same $c$ than water) from $20^oC$ to $100^oC$? Answer: $\Delta Q $ $= $ $c\cdot m\Delta T $ $\Delta Q $ $= $ $1\cdot 600 \cdot (100$ $-$ $20)$ $ =$ $ 48000\; cal $ $=$ $48\; kcal$ $\frac{48}{4}$ $=$ $12\;g$ of sugar must be burnt, that means 4 lumps!
