The energy of a chemical bond (enthalpy of dissociation of a bond) is the variation of enthalpy of the reaction which dissociates one mole of such bonds..
At $25^oC$ and 1 bar $436\;kJ$ heat must be given to one mole of hydrogen gas to dissociate it to 2 moles of single hydrogen atoms : $H_2(g)$ $\longrightarrow$ $2H(g)$ $\Delta H$ $=$ $+436\; kJ$ The energy of the $H-H$ bond (= the enthalpy of the dissociation reaction of $H_2$) = $436\;kJ$ !!
The same type of bond is often found in numerous different molecules, the $C-H$ bond for instance is present in the molecules $CH_4$, $C_2H_6$, $C_{10}H_{22}$.. The environment in all those molecules is slightly different, so that the enthalpy of dissociation will also be slightly different. See the → Table of averages of the usual energies of a bond .
Many bond energies have been determined. They allow to calculate approximately most "reaction heats" $(= -\Delta H_{reaction})$ and "transformation heats" $(= -\Delta H_{transformation})$ if the bonds present in reagents and products are known.
Let us calculate approximately the heat of the following reaction : $2H_2O(g)$ $+$ $2Cl_2(g)$ $\longrightarrow$ $4HCl(g)$ $+$ $O_2(g)$
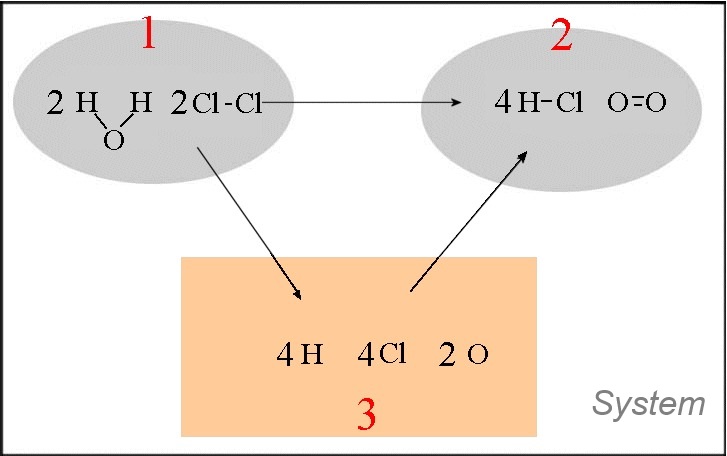
- In the orange box are written the single atoms - The transformations $1\rightarrow 3$ and $2\rightarrow 3$ are dissociation reactions of chemical bonds ! $\Delta H_{12}$ $=\Delta H_{13}$ $+$ $\Delta H_{32}$ $=\Delta H_{13}$ $-$ $\Delta H_{23}$ $=(4\cdot E_{bond}(H-O)$ $+$ $2\cdot E_{bond}(Cl-Cl))$ $-$ $(4\cdot E_{bond}(H-Cl)$ $+$ $E_{bond}(O=O))$ $=4\cdot 465$ $+$ $2\cdot 243 $ $- $ $(4\cdot 431$ $ +$ $494)$ $=128\;kJ$ Note that this result is slightly different from the (more correct) value found with standard enthalpies of formation ($114.4\; kJ)$!
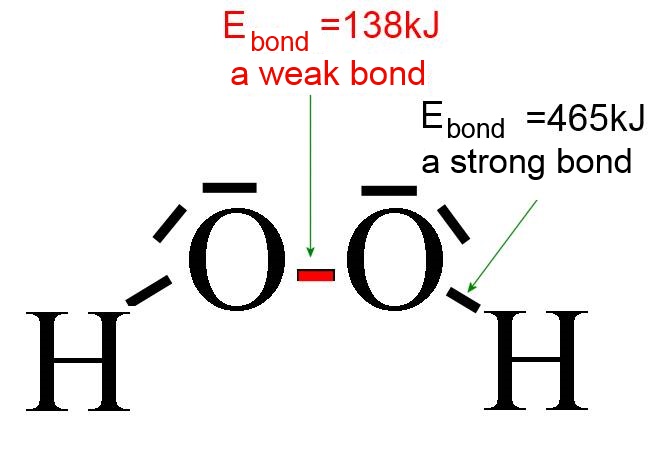
The bond energy is a good measure for the "strength" of bonds ( = the tear resistance), for instance in the hydrogen peroxide molecule, where the O-O is weak: