The element iron is found in three states:
The metallic iron, symbol: $Fe$, here under the form of nails.
The iron(II) ion, symbol: $Fe^{2+}$, here for instance present in the ionic substance iron(II) sulfate.
The iron(III) ion, symbol: $Fe^{3+}$, here for instance present in the ionic substance iron(III) chloride.
In the iron(III) ion, the element iron is more oxidised (has lost more electrons !) than in the iron(II) ion where it is still more oxidised than
in metallic iron:
The oxidation state is caracterised by a number called oxidation number
o.n.($Fe^{3+}$)= $3$ o.n.($Fe^{2+}$)=$2$ o.n.($Fe$)= $0$
Oxydation number of a neutral atom = 0 Oxydation number of a monoatomic ion = its charge
o.n.($Cl^{-}$)= $-1$ o.n.($S^{2-}$)= $-2$ o.n.($Al^{3+}$)= $3$ o.n.($Mg$)= $0$
This definition is extended to polyatomic ions and molecules:
Oxidation number of a (neutral !) molecule = 0 Oxidation number of a polyatomic ion = its charge
o.n.($Cl_2$)=0 o.n.($SO_4^{2-}$)= $-2$ o.n.($NH_4^{+}$)= $1$ o.n.($H_2O_2$)= $0$
It is useful to introduce an oxidation number for each atom inside a polyatomic ionor a molecule. A rough estimate is made that the species would be wholly dissociated to ions:
The electrons of every bond are given to the more electronegative atom. In case the atoms have the same electronegativity, every atom gains one electron of the bond. The resulting charge of the atom gives its oxidation number.
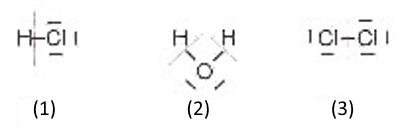
(1) The 2 electrons of the bond are gived to the chlorine atom which has now 8 electrons in its outer layer (one more than in the Lewis structure of the neutral atom) The hydrogen atom has now 0 electrons in its outer layer (one less than in the Lewis structure of the neutral atom): o.n.($H$ in $HCl$) = $1$ o.n.($Cl$ in $HCl$)= $-1$ (2)The 4 electrons of the two bonds are gived to the oxygen atom which has now 8 electrons in its outer layer (2 more than in the Lewis structure of the neutral atom) Each hydrogen atom has now 0 electrons in its outer layer (one less than in the Lewis structure of the neutral atom): o.n.($H$ in $H_2O$= $ 1$) o.n.($O$ in $H_2O$= $-2$ (3) One electron of the bond is given to each chlorine atom which has now 7 electrons in its outer layer (the same number than in the Lewis structure of the neutral atom) o.n.($Cl$ in $Cl_2$)=$ 0$
The previous examples lead us to the following pratical rules:
O.n of $H$ in a compound species (ion or molecule) = 1 O.n of $O$ in a compound species (ion or molecule) = -2 O.n of $F,Cl,Br,I,$ in a compound species (ion or molecule) = -1
The first rule applies only in case $H$ is the less electronegative atom, the second and third in case $O,F,Cl,Br,I$ are the more electronegative in the bond where they are engaged.
o.n.($H$) in $C_2H_6$ $=$ $1$ o.n.($H$) in $H_2$= $0$ o.n.($Cl$) in $ClBr$= $-1$ o.n.($Br$) in $ClBr$=+1 ! It should be observed furthermore that: o.n.($H_2O$)=0 =$2\cdot$o.n.($H$ in $H_2O$)+o.n.($O$ in $H_2O$) o.n.($OH^{-}$)=$-1$ =o.n.($O$ in $OH^-$)+o.n.($H$ in $OH^-$)
The sum of the oxidation numbers of all atoms in a molecule = 0 The sum of the oxidation numbers of all atoms in a polyatomic ion = its charge
These rules can be used in simple calculations, for example: Calculate the o.n.(S in $SO_2$)! Let's call this oxidation number $x$: $x$ $+$ $2(-2)$ $=$ $0$ $x$ $=$ $4$ Indeed: The o.n.(O) in this molecule = -2 and the sum of oxidation numbers of the whole molecule = 0 Calculate the o.n.(N in $NO_3^-$)! Let's call this oxidation number $x$: $x$ $+$ $3(-2)$ $=$ $-1$ $x$ $=$ $5$ Indeed: The o.n.(O) in this polyatomic ion = $-2$ and the sum of oxidation numbers of the whole $NO_3^-$ ion $-1$
Example: Oxidation numbers in the synthesis of aluminium bromide:
| $Al$ | $-3e^-$$\longrightarrow $ | $ Al^{3+}$ | (1) | $0$ | $3$ | $Br_2$ | $+2e^-$$\longrightarrow $ | $2 Br^{-}$ | (2) | $2\cdot 0$ | $2\cdot -1$ |
When the oxidation number decreases by n units, the species takes n electrons When the oxidation number increases by n units, the species loses n electrons
..which is a very logical rule, since we have assimilated the oxidation number to a fictitious charge!
Example: Oxydation numbers in the reduction of the peroxodisulfate ion:
| $S_2$$O_8^{2-}$ | $......$$\longrightarrow $ | $2S$$O_4^{2-}$ | (1) | $2\cdot7$ | $2\cdot6$ |