





A heterogeneous equilibrium is a chemical equilibrium between species present in different phases. At least one of the species must have a constant concentration in one of its phases.
Let's suppose that reagent $Y$ occurs in the solid phase, the reagent $X$ and the products $C$ and $D$ in a gaseous phase: $aX_{(g)}+b$ $Y_{(s)}$$ \leftrightarrows$ $cC_{(g)}$ $+$ $dD_{(g)} $ (1) The reaction is only possible if $Y$ passes first from the solid phase into the gaseous phase: $Y_{(s)}$$\leftrightarrows$$Y_{(g)}$ (2) Now we have a homogeneous equilibrium (1) as well as a heterogeneous one (2):
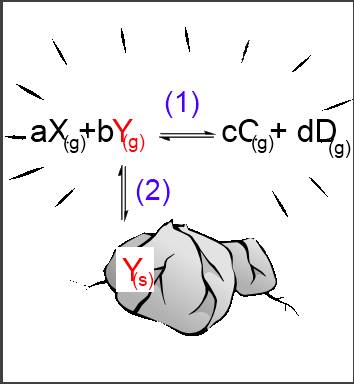
Let's apply the laws of mass action to these two equilibria: (1): $\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a\cdot[Y_{(g)}]^b}$ $=$ $K_c $ (2): $[Y_{(g)}]$ $=$ $K_{sat} $ (2) into (1) : $\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a\cdot K_{sat}^b}$ $=$ $K_c $ $\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a}$ $=$ $K_c\cdot K_{sat}^b $ $ K_c\cdot K_{sat}^b$ is a new constant $K$, so that:
In case of an heterogeneous equilibrium $aX_{(g)}$ $+$ $b$ $Y_{(s)}$$ \leftrightarrows$ $cC_{(g)}$ $+$ $dD_{(g)} $, the following applies: $\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a}$ $=$ $K $ In the law of mass action, one leaves out the species present in the phase where its concentration is constant!