






In this experiment the color (concentration!) of a reagent decreases over time. In physics, rate of travel (velocity) of a mobile is defined as the ratio between distance ( = variation of distance) and time necessary to cover that distance ( = variation of time). By analogy, in chemistry, the rate of a reaction is defined as the ratio between the variation of concentration and time necessary to cover that variation ( = variation of time).
If $\Delta [X]$ means the variation of the molarity of a reactant X ( = final molarity - initial molarity!), a negative parameter (as the molarity of the reactant X decreases), and $\Delta t$ the time necessary to cover that variation, then:
Rate of a chemical reaction in relation to a reagent X : $v_X$ $=$ $- \frac{\Delta [X]}{\Delta t}$
(The minus sign "-" comes from the fact that we want the rate to be positive ! )
If the rate was defined in relation to a product Y of the reaction, the minus sign would have to be let aside as the molarity of this reagent increases ! $v_Y$ $=$ $\frac{\Delta[Y]}{\Delta t}$
The rate we have defined before is the average rate between two instants $t_i$ (initial time) and $t_f$ (final time) with $\Delta t$ $=$ $t_f - t_i$.
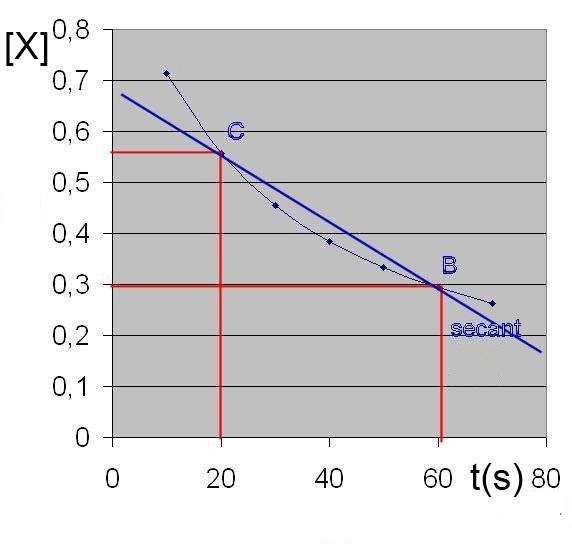
Average rate between C and B = $-\frac{[X_f]-[X_i]}{t_f-t_i}$ = - slope of the line passing through C et B
(in our case) = $-\frac{0.3-0.56}{60-20}$ = $0.0065$ $\frac{mol}{L\cdot s}$
If that difference is made very small, we get the "instantaneous" rate.
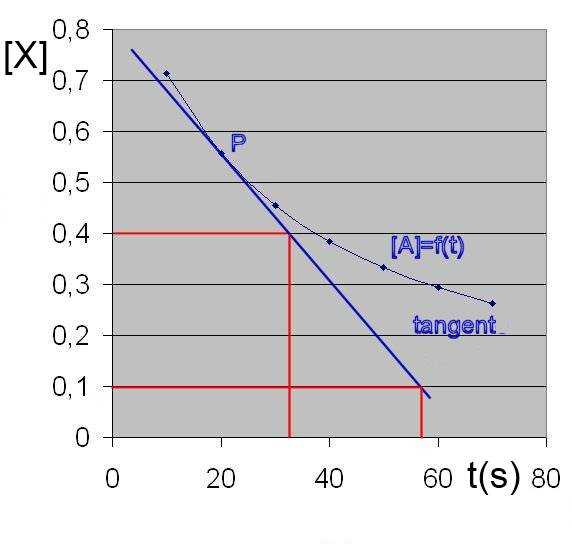
Instantaneous rate at point P = -slope of the tangent in P
(in our case) = $-\frac{0.1-0.4}{56-32}$ = $0.0125$ $\frac{mol}{L\cdot s}$