





Vodka is a mixture of alcohol with water.

Water is the solvent Alcohol is the solute, (symbol: $so$) Vodka is the solution, (symbol: $S$)
The mass density of the solution is the result of dividing the mass of the solution by its volume:
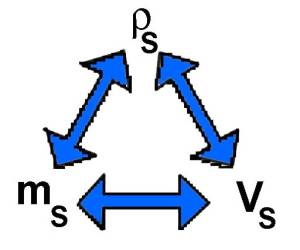
Mass density of the solution $\rho_S=\frac{m_S}{V_S}$
For instance $\rho_{S}$ $=$ $0,95\frac{g}{cm^{3}}$ means that $1cm^3$ solution S has a mass of $0,9 g$ In this case, we have indeed: $\rho_{S}$ $=$ $\frac{0,95}{1}$ $=$ $0,95\frac{g}{cm^{3}}$
The number of moles of solute is the result of dividing the mass of solute ( g ) by its molar mass.
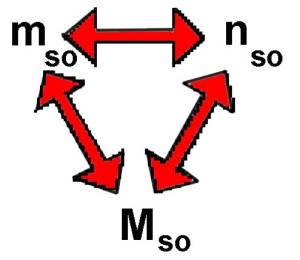
Number of moles of solute: $n_{so}$ $=$ $\frac{m_{so}}{M_{so}}$
For instance 18 g glucose $(C_6H_{12}O_6)$ are $n_{glucose}$ $=$ $\frac{18}{6\cdot 12+12\cdot 1+ 6\cdot 16}$ $=$ $0,1 $ mol
The percentage of solute is the result of dividing the mass of solute by the mass of the solution, and then multiplying by $100$
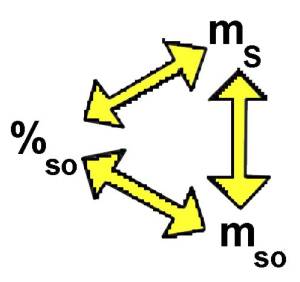
Percentage of solute: $\%_{so}$ $=$ $\frac{m_{so}\cdot 100}{m_S}$
For instance, $\%_{so}=24$ means that $100 g$ solution $S$ contain $24 g$ solute $so$ In this case, we have indeed: $\%_{so}$ $=$ $\frac{24\cdot 100}{100}$ $=$ $24$
The molarity of the solute is the result of dividing the number of moles of the solute by the volume of the solution.
Molarity of the solute: $[so]$ $=$ $\frac{n_{so}}{V_S}$
For instance, $[so]$ $=$ $2\frac{mol}{L}=2M$ (not to be confused with the molar mass M!) means that $1 L$ solution $S$ contains $2 mol$ solute $so$ In this case, we have indeed: $[so]$ $=$ $\frac{2}{1}$ $=$ $2\frac{mol}{L}$
Each colored triangle corresponds to one of the preceding formulas:
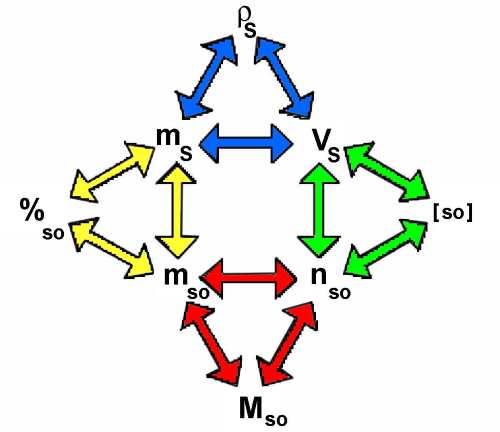
In such a triangle one parameter may be calculated knowing the other two. The diagrams allows to pass from one triangle to the other.
Example:
$3\; L$ of a solution with mass density $\rho_{S}=1,2\frac{g}{cm^3}$ contain $2 \;mol$ of a solute with molar mass $M_{so}=72\frac{g}{mol}$. Calculate the percentage of solute in this solution!
Answer:
$3L$ $=$ $3000cm^3$ $\rho_S$ $=$ $\frac{m_S}{V_S}$ $ m_S$ $=$ $\rho_S\cdot V_S$ $m_S$ $=$ $1,2\cdot 3000$ $=$ $3600 g$
$n_{so}$ $=$ $\frac{m_{so}}{M_{so}}$ $m_{so}$ $=$ $n_{so}\cdot M_{so}$ $m_{so}$ $=$ $2\cdot 72$ $=$ $144 g$
$\%_{so}$ $=$ $\frac{m_{so}\cdot 100}{m_S}$ $\%_{so}$ $=$ $\frac{144\cdot 100}{3600}$ $=$ $4$ Percentage of solute = $4\%$ .