





(about variation of volume and pressure during a transformation of a fixed quantity of gas at a fixed temperature).
The volume is changed by means of the piston, the manometer measures the pressure:

Results:
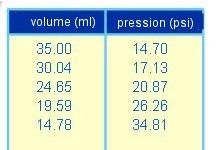
The product of pressure by volume is constant!
At a constant temperature: $P \cdot V$ $=$ $k_1$ where $k_1$ is a constant at a given temperature.
The transition of a given gas at fixed temperature from state 1 (pression $P_1$, volume $V_1$) to state 2 (pression $P_2$, volume $V_2$), obeys therefore to the law:
At constant temperature: $P_1 \cdot V_1$ $=$ $P_2 \cdot V_2$ ( = $k_1$)
(about variation of volume and temperature during a transformation of a fixed quantity of gas at a fixed pressure).
The volume is changed by means of the stove, a thermometer measures the temperature:

Results:

The fonction V=f(t) is a straight line which intersects the temperature-axis at $-273.15^oC $
If a new scale of temperatures is defined by:
Absolute temperature = Kelvin temperature = $T = 273.15 + t^oC$
then the origin $T = 0 K$ is reported to $-273.15^oC $ and the diagram V=g(T) is a straight line passing through the origin of the axes:
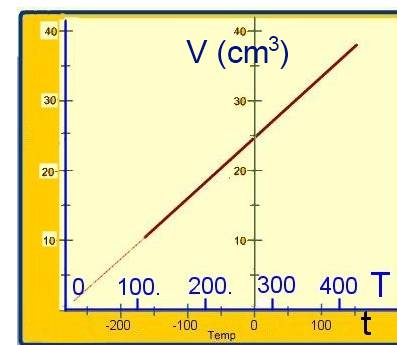
$V = k_2T$ where $k_2$ is a constant at a given pressure.
The transition of a given gas at fixed pressure from state 1 ( Kelvin temperature $T_1$, volume $V_1$) to a state 2 ( Kelvin temperature $T_2$, volume $V_2$), obeys therefore to the law:
At a constant pressure: $\frac{V_1}{T_1}$ $=$ $\frac{V_2}{T_2}$ ( = $k_2$)
(about variations of volume, pressure and temperature during a transformation of a fixed quantity of gas) .
Let's consider a transformation of a gas from a state 1 to a state 2:
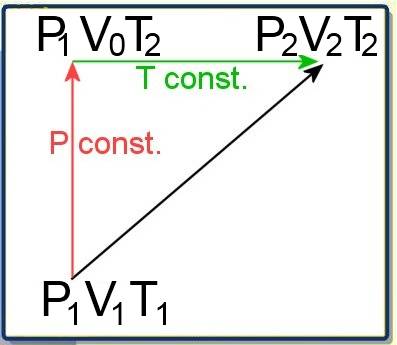
Let $P_1$ , $V_1$ and $T_1$ be the pressure , volume and temperature in state 1. Let $P_2$ , $V_2$ and $T_2$ be the pressure , volume and temperature in state 2. The transition from 1 ŕo 2 may also be realised by a detour consisting in a transformation at fixed pressure (a) followed by a transformation at fixed temperature (b) (a)$\frac{V_1}{T_1}$ $=$ $\frac{V_0}{T_2}$ (Gay-Lussac) (b)$P_1\cdot V_0$ $=$ $P_2\cdot V_2$ (Boyle-Mariotte) Eliminating $V_0$ between (a) and (b) gives:
$\frac{P_1\cdot V_1}{T_1}$ $=$ $\frac{P_2\cdot V_2}{T_2}$
(about the description of one gas state : volume, pressure, temperature and mole number) .
Let's consider one mole of gas. The ideal gas law form 1 applies to this case. $\frac{P_1\cdot V_1}{T_1}$ $=$ $\frac{P_2\cdot V_2}{T_2}$ At any temperature and pressure and for one mole gas, the product $\frac{P\cdot V}{T}$ remains constant: $\frac{P\cdot V}{T}$ $=$ $R$ $V$ $=$ $R\frac{T}{P}$ where $R$ is a constant for one mole of gas depending no more on pressure and temperature) $R$ $=$ $0.082\frac{l\cdot atm}{mol\cdot K}$ if $P$ is expressed in atmospheres and $V$ in litres $R$ $=$ $8.3\frac{N\cdot m}{mol\cdot K}$ if $P$ is expressed in Pascal ($\frac{N}{m^2}$) and $V$ in $m^3$ For n moles of gas, in the same conditions of temperature and pressure, according to d'Avogadro's law, the volume is multiplied by n : $V$ $=$ $n\cdot R\frac{T}{P}$ or :
$P\cdot V$ $=$ $n\cdot R\cdot T$ $R$ $=$ $0.082\frac{l\cdot atm}{mol\cdot K}$ $R$ $=$ $8.3\frac{N\cdot m}{mol\cdot K}$
(about the volume and number of moles of a gas at 0oC and 1 atm = the normal conditions of temperature and pressure).
Let's apply the ideal gas law (form 2): $P\cdot V$ $=$ $n\cdot R\cdot T$ $1\cdot V$ $=$ $n\cdot 0.082\cdot 273.15$
At 0oC and 1 atm (NTP): $V$ $=$ $n\cdot 22.4$ where $V$ is expressed in litres