Die Symmetrie der Moleküle ist in der → Stereochemie von wesentlicher Bedeutung Symmetrie ist auch essentiell in der → Kristallographie
Zwei Figuren sind gegenseitig symmetrisch , wenn sie übereinandergelegt werden können durch eine geometrische Operation, die unter Verwendung von Symmetrieelementen genannten Operatoren ausgeführt wird:
|
|
|
|
| Punkt | I | Zentrale Symmetrie |
| Ebene | M bezeichnet σ | Spiegel |
| Rotationsachse* | A2 noch bezeichnet C2 oder 2 A3 noch bezeichnet C3 oder3 A4 noch bezeichnet C4 oder 4 A6 noch bezeichnet C6 oder 6 |
Rotation um 180° Rotation um 120° Rotation um 90° Rotation um 60° |
* die Rotation-Inversionsachsen werden durch die Kombination aus einer Achse und eine Symmetriezentrum aus. die Rotation-Reflexionsachsen werden durch die Kombination einer Achse und eine Symmetrieebene gekennzeichnet.
Beispiele von Symmetriezentren I
Der gesamte Rahmen hat das Symmetriezentrum I A' Bild von A B' Bild von B
Das Molekül Cuban $ C_8H_8$ hat das Symmetriezentrum I
Dieser Pyritkristall $ FeS_2$ hat im Symmetriezentrum I
Beispiele für Symmetrieebene M (noch bezeichnet σ)
Der Frosch hat die Symmetrieebene M (noch bezeichnet σ) A' Bild von A B' Bild von B C' Bild von C
Das Formaldehyd-Molekül (methanal) $ CH_2O$ hat zwei Symmetrieebenen M1 (noch bezeichnet σ 1) und M2 ( noch bezeichnet σ 2) .
Dieser Kristall Vivianit $Fe^{2+}_3(PO_4^{3-})_2 · 8H_2O $ besitzt die Symmetrieebene M (noch bezeichnet σ) .
Beispiel von Symmetrieachsen A2 noch bezeichnet C2 oder 2
Die alten Amphore hat vier paarweise gegenüberstehende Griffe . Da die Griffe nicht ganz im rechten Winkel zueinander stehen, hat es eine Symmetrieachse der Ordnung 2 A2 noch bezeichnet C2 oder 2 .
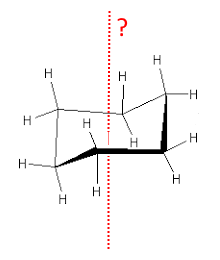
Diese Bootkonformation des 1,3-Dichlorcyclohexan hat eine Symmetrieachse der Ordnung 2 A2 noch bezeichnet C2 oder 2 Es sind alle Atome voneinander durch eine Drehung von 180 $ ^ o $ um diese Achse abgeleitet.
Dieser Selenit $ Ca^{2+} SO_4^{2-}· 2H_2O$ hat eine Symmetrieachse der Ordnung 2: A2 noch bezeichnet C2 oder 2 .
Beispiel von Symmetrieachsen A3 noch bezeichnet C3 oder 3
Der Tetraeder vom Strand von Pen Bron hat eine Symmetrieachse der Ordnung 3: A3 noch bezeichnet C3 oder 3 A' Bild von A .
Das Ammoniakmolekül $ NH_3 $ hat eine Symmetrieachse der Ordnung 3: A3 noch bezeichnet C3 oder 3 .
Quarz $ SiO_2 $ hat eine Symmetrieachse der Ordnung 3: A3 noch bezeichnet C3 oder 3 .
Beispiel von Symmetrieachsen A4 noch bezeichnet C4 oder 4
Die Cheops Pyramide hat eine Symmetrieachse der Ordnung 4: A4 noch bezeichnet C4 oder 4 .
Das Pentaboranmolekül (9) $ B_5H_9$ hat eine Symmetrieachse der Ordnung 4: A4 noch bezeichnet C4 oder 4 .
Kassiterit $ SnO_2$ hat eine Symmetrieachse der Ordnung 4: A4 noch bezeichnet C4 oder 4 .
Beispiel von Symmetrieachsen A6 noch bezeichnet C6 oder 6
Die alte Kirche Unserer Lieben Frau von Nazareth hat eine Symmetrieachse der Ordnung 6: A6 noch bezeichnet C6 oder 6 .
Das Molekül Benzol $ C_6H_6$ hat eine Symmetrieachse der Ordnung 6: A6 noch bezeichnet C6 oder 6 .
Der Smaragd $Be_3(Al,M)_2(SiO_3)_6, \; (M \; = \, Cr, Fe, V) $ hat eine Symmetrieachse der Ordnung 6: A6 noch bezeichnet C6 oder 6 .
Rotation-Inversionsachsen werden durch die Kombination aus einer Rotation und einer Inversion definiert. Hinweis: Die Rotations-Inversion der Ordnung 1 setzt sich aus einer 360°-Winkelrotation und einer Inversion zusammen: $\bar{1}= \;i $ . Die als Beispiel angeführte Rotations-Inversion der Ordnung 2 ist tatsächlich eine Spiegelung an der Spiegelebene senkrecht zur Rotationsachse, die durch das Inversionszentrum geht: $\bar{2}=\sigma $ .
Die Dreh-Spiegel-Achse sind durch die Kombination einer Achse und einer zu dieser Achse senkrechten Symmetrieebene gekennzeichnet.
Das Tetraeder hat eine Dreh-Spiegel-Achse der Ordnung 4: : $S4$ : Der Punkt $A$ ergibt sich durch Drehung um $90^ o$ der Punkt X (1), der seinerseits durch Spiegelung an der Ebene den Bildpunkt $A'$ (2) ergibt.
Hinweis:
Da der Spiegel (Reflexion von der Ebene) einer Drehung von π gefolgt von einer Inversion, eine Rotationsreflexion (per Definition eine Rotation von &thgr;, gefolgt von einem Spiegel) ist daher eine Rotationsinversion des Winkels &thgr; + π
Die Rotationsreflexion der Ordnung 1 ist also ein Spiegel: $S1= \sigma $ .
Die Rotationsspiegelung der Ordnung 2 ist also eine Inversion: $S2= \;i $ .
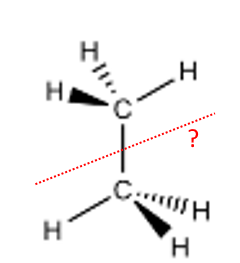
Finden Sie die vertikale Rotationsachse (klicken)
Finden Sie die Anzahl der Spiegel (klick)
Finden Sie die Anzahl der Rotations-Reflexionsachsen (klicken)
Klicken Sie auf die folgenden Abbildungen, um das dargestellte Symmetrieelement zu identifizieren:
