






Eine Sammellinse (konvergente Linse) ist eine bikonvexe Linse, die ein invertiertes Bild eines Objekts bildet (wie die Dunkelkammer!)..


Die Linse ist folgendermassen schematisiert. Der Punkt $ A_1 $ ist das Bild des Punktes $ A $
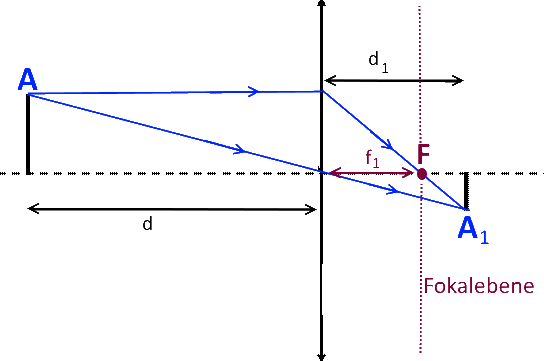
Jeder $ A $ -Punkt im Objekt sendet Lichtstrahlen in alle Richtungen aus Wir können zeigen: - Alle von $ A $ ausgestrahlten Strahlen, die durch die Linse laufen, laufen am selben Punkt $ A_1 $ zusammen - Der durch das optische Zentrum tretende Strahl wird nicht abgelenkt. - Der zur optischen Achse parallele Strahl schneidet diese an einem Punkt $ F $, der den Fokus der Linse darstellt. - Die Brennweite $ f_1 $ ist eine Eigenschaft des betreffenden Objektivs. Es hängt nicht von der Position des Punktes $ A $ ab, also ist es für alle Punkte gleich, nach denen wir nach dem Bild suchen!
Es gibt ein Gesetz, das die Brennweite $ f_1 $ mit den Entfernungen $ d $ und $ d_1 $ der Objekt- und Bildpunkte zur Objektivachse verbindet. Wir können zeigen:
$\frac{1}{d}$ $+$ $\frac{1}{d_1}$ $=$ $\frac{1}{f_1}$
Für $d\rightarrow\infty$, hat man: $\frac{1}{d}\rightarrow 0$ und also: $d_1\approx f_1$
Wenn das Objekt weit entfernt ist, befindet sich das Bild in der Fokalebene!