





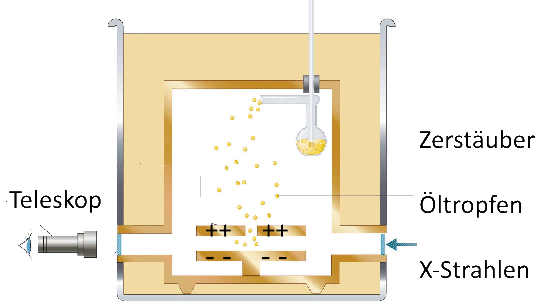
$ M $ Öltröpfchen fallen in ein elektrisches Feld $ E $. Einige bleiben zwischen den Platten hängen. Dies sind (wahrscheinlich) diejenigen, die ein Elektron durch Röntgenstrahlen eingefangen haben, die also eine negative Elementarladung $ e $ haben Ihr Gewicht muss gleich der elektrischen Kraft sein, die sie zurückhält! Wir haben: $M\cdot g$ $=$ $e\cdot E$ $\frac{M}{e}$ $=$ $\frac{g}{E}$ (1)
Wenn y Funktion von x ist, dann besitzt die Differentialgleichung $\frac{dy}{dx}$ $=$ $ay$ $+$ $b$ eine Lösung: $y$ $=$ $e^{ax}$ $-$ $\frac{b}{a}$ (2) In der Tat, dann ist $\frac{dy}{dx}$ = $ae^{ax}$ = $a(y$ $+$ $\frac{b}{a})$ = $ay$ $+$ $b$

Die Öltröpfchen fallen ohne ein elektrisches Feld. Dann üben sich zwei Kräfte auf sie aus: 1) das Gewicht $ P = $ $ M \cdot g $ 2) die Reibungskraft $ F = $ $ \gamma \cdot v $ wo $ \gamma $ der Reibungskoeffizient ist Die resultierende Kraft ist daher: $P$ $-$ $F$ $=$ $M\cdot g$ $-$ $\gamma \cdot v$ Nach Newtons Gesetz haben wir: $M\cdot \frac{dv}{dt}$ $=$ $M\cdot g$ $-$ $\gamma \cdot v$ $ \frac{dv}{dt}$ $=$ $g$ $-$ $\frac{\gamma}{M} \cdot v$ was eine Differentialgleichung vom Typ (2) ist mit $a$ $=$ $-\frac{\gamma}{M} $ und und daher die Lösung: $v$ $=$ $\frac{Mg}{\gamma}(1+e^{-\frac{\gamma \cdot t}{M}})$ Da $ \gamma $ groß und $ M $ klein ist, tendiert der zweite Term schnell zu 0 und für die beobachtete stationäre Geschwindigkeit $ v $ haben wir: $V$ $=$ $\frac{Mg}{\gamma}$ (3) Diese Gleichung ermöglicht somit die Bestimmung von $ M $ und mit (1) auch $ e $ ! Wir finden:
$e$ $=$ $1,6\cdot 10^{-19}\;C$