Die möglichen Zustände der Elektronenenergie in einem Atom werden durch die bekannten Quantenzahlen $ n $, $ l $, $ m $ und $ s $ nummeriert. Einige Atomkerne, zum Beispiel derjenige des Atoms $ ^1H $ (das normale Isotop von Wasserstoff), können auch verschiedene energetische Zustände annehmen, vorausgesetzt, sie sind einem starken Magnetfeld ausgesetzt. Im Gegensatz zu Atomenergieniveaus hängen diese Werte von der Intensität des Magnetfelds ab, dem die Kerne ausgesetzt sind. Beispielsweise stellt der Kern $ ^1H $ zwei energetische Zustände dar, sobald er einem Magnetfeld $ H $ ausgesetzt ist und die Energiedifferenz $ \Delta E $ zwischen diesen beiden Zuständen steigt an, wenn wir die magnetische Intensität des Feldes erhöhen .
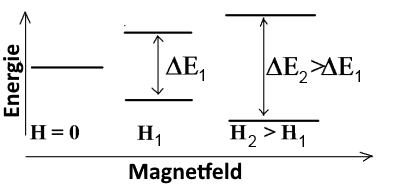
Nach dem Planckschen Gesetz absorbiert der Wasserstoffkern - in einem Feld $ H_1 $ elektromagnetische Strahlung(normalerweise im Radiofrequenzbereich) der Frequenz $ \nu_1 = \frac{\Delta E_1}{h} $ - in einem Feld $ H_2 $ die Frequenzstrahlung $ \nu_2 = \frac {\Delta E_2}{h} $

Selbst wenn wir ein streng konstantes Magnetfeld auf eine Materialprobe mit $ ^1H $-Atomen anwenden, erfahren die Kerne all dieser Atome nicht das gleiche Feld, da das äußere Feld durch die elektronische Umgebung dieser Atome verändert wird . Je nach dieser elektronischen Umgebung werden wir beobachten, dass eine Strahlung mit einer anderen Frequenz absorbiert wird! Dies erklärt die Möglichkeit, indem man die Probe (zusätzlich zum konstanten Magnetfeld) erhöhten Radiofrequenzen unterwirft, die von den Atomen $ ^ 1H $ mehr oder weniger absorbiert werden, Spektren aufzunehmen, mit denen man die Atome $^1H $ mit einer anderen elektronischen Umgebung unterscheiden kann. .
Das äußere Feld eines Kerns wird durch die elektronische Umgebung dieser Kerne verändert. Durch das "Umlaufen" des Kerns $^1H $ erzeugen die Elektronen ein Richtungsfeld entgegen der Richtung des angelegten Feldes (siehe Physik: Induktion usw.) und verringern so die Intensität des an den Kernen angelegten Feldes. $ \Delta E $ wird reduziert und damit die absorbierte Frequenz $ \nu $: Je mehr der Wasserstoffkern von Elektronen umgeben ist ("abgeschirmt"), desto schwächer ist die von ihm aufgenommene Hochfrequenz! Zur Bewertung dieser Abschirmung wird in der Praxis eine Referenzsubstanz mit der zu analysierenden Probe gemischt, deren Atome die gleiche Abschirmung aufweisen, z. B. Tetramethylsilan $(CH_3)_4Si$ oder Dimethylsulfoxid $(CH_3)_2SO $, die bei einer gegebenen Frequenz $ \nu_{ref} $ absorbieren. Dann ermitteln wir den relativen Unterschied zwischen der Absorptionsfrequenz des Wasserstoffs, an dessen Abschirmung wir interessiert sind, und der Referenzfrequenz. Diese Lücke wird chemische Verschiebung $ \delta $ genannt:
Chemische Verschiebung (ausgedrückt in $ppm$ Teile pro Million): $\delta=\frac{\nu - \nu_{ref}}{\nu_{ref}}\cdot 10^6$
Hier zum Beispiel das NMR-Spektrum von Methylethanoat:
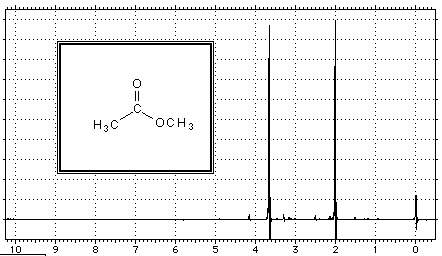
Bei $ \delta = 0 $ finden wir die Absorptionslinie der $ H $ -Atome des der Probe hinzugefügten Tetramethylsilans, bei $ \delta = 2,00 $ der der $ H $ -Atome der Methylgruppe $ CH_3 $, bei $ \delta = 3,65 $ der der $ H $ -Atome der Methoxy $ OCH_3 $ - Gruppe.
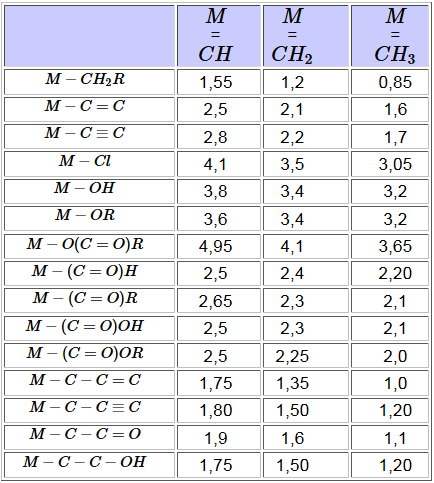
- Der negative induktive Effekt $ I- $ von stark elektronegativen Atomen verringert die Abschirmung und erhöht $ \delta $ (siehe zum Beispiel den Effekt des O-Atoms der $ OCH_3 $ - Gruppe !) - Der positive induktive Effekt $ I+ $ von hochelektropositiven Atomen oder Alkylketten erhöht die Abschirmung und verringert $ \delta $ (siehe zum Beispiel die Wirkung des $Si$-Atoms von Tetramethylsilan!) - Der mesomere Effekt kann wichtig sein.
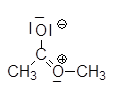
Diese mesomere Grenzstruktur mit ihrer positiven Ladung an Stickstoff erklärt sicherlich die verringerte Abschirmung der $ H $ -Atome des $ OCH_3 $!

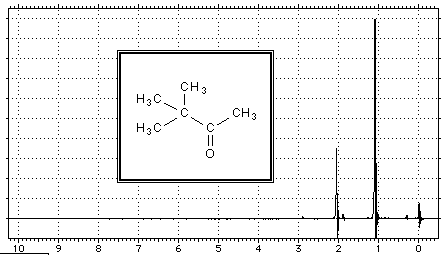
Die 9 H-Atome der linken Methylgruppen im vorherigen Beispiel haben eine äquivalente elektronische Umgebung (tetraedrische Kohlenstoffstruktur, freie Rotation der DC-Bindung). Der Peak $ \delta = 1,1$ dieser Atome hat eine 3 mal größere Oberfläche als der Peak bei $ \delta = 2,05$ am H der anderen Methylgruppe. Die Fläche der Peaks ist proportional zur Anzahl der entsprechenden H-Atome.
Schauen wir uns das System an, das nur aus diesen drei $H$ - Atomen besteht :

Wir wissen, dass der Kern jedes Atoms $H$ sich in zwei Zuständen (Energieniveaus) befinden kann. Nennen wir diese Zustände (Spins) mit +1/2 und -1/2. 1) Was kann der linke Wasserstoff "sehen", indem er auf die beiden Wasserstoffatome rechts "schaut"? (Besser: Welchen Einfluss haben die elektronischen Wolken des rechten $ H $ auf den linken $ H $?) Antwort:

Er "sieht" drei verschiedene Konfigurationen (1), (2) und (3) mit den Frequenzen 1: 2: 1! Jede dieser Konfigurationen beeinflusst die chemische Verschiebung unterschiedlich: Ihr Peak trennt sich in ein Triplett! 2) Was können die (äquivalenten) Wasserstoffatome auf der rechten Seite "sehen", wenn sie den einzigen Wasserstoff auf der linken Seite "betrachten?" Antwort:
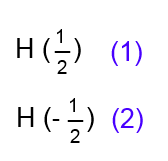
Sie "sehen" zwei verschiedene Konfigurationen (1) und (2) mit den Frequenzen 1: 1! Jede dieser Konfigurationen beeinflusst ihre chemische Verschiebung unterschiedlich: Ihr Peak wird sich im Dublett trennen! Die Gesamtfläche des Tripletts ist nur halb so groß wie die des Dubletts, da das Triplett nur von einem $ H $ -Atom stammt, das absorbiert, während das Dublett von zwei kommt! Im Triplett stehen die Flächen im Verhältnis 1: 2: 1! Im Dublett liegen die gleichen Flächen im Verhältnis der Frequenzen 1: 1.
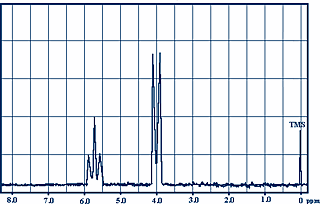
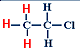
1,1,2-Trichloroethan
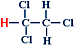
Schauen wir uns das System an, das nur aus diesen fünf $H$ Atomen besteht :

1) Was kann jeder der linken Wasserstoffe "sehen", wenn auf die beiden Wasserstoffe rechts "schaut"? (Besser: Welchen Einfluss haben die elektronischen Wolken des rechten $ H $ auf jeden verbleibenden $ H $?) Antwort:

Er "sieht" drei verschiedene Konfigurationen (1), (2) und (3) mit den Frequenzen 1: 2: 1! Jede dieser Konfigurationen beeinflusst die chemische Verschiebung unterschiedlich: Ihr Peak trennt sich in ein Triplett! 2) Was können die (äquivalenten) Wasserstoffatome "sehen", wenn sie die drei Wasserstoffatome auf der linken Seite "betrachten "? Antwort:

Sie werden vier verschiedene Konfigurationen (1) und (2) sowie (3) und (4) mit den Frequenzen 1: 3: 3: 1 sehen! Jede dieser Konfigurationen beeinflusst ihre chemische Verschiebung unterschiedlich: Ihr Peak wird in ein Quadruplett getrennt!
Die Gesamtfläche des Quadrupletts beträgt nur zwei Drittel der Fläche des Tripletts, da das Tripel von drei Atomen $ H $ stammt, die absorbieren, während das Quadruplet nur von zwei kommt! Im Quadruplett stehen die Flächen im Verhältnis 1: 3: 3: 1! Im Triplett stehen die Flächen im Verhältnis 1: 2: 1!

Chloroethan