Man mischt $100\; mL$ $NaOH$ $0,1\; M$ mit $900\; mL$ Diethylamin $0,1\; M$
a)Stellen Sie für diese Mischung 5 Gleichungen zwischen Gleichgewichtsmolaritäten her :
$[Na^+]$, $[H_3O^+]$, $[(C_2H_5)_2NH]$, $[(C_2H_5)_2NH_2^+ ]$, et $[OH^-]$
(Die Bedingung der Elektroneutralität, zwei Bedingungen der Erhaltung der Materie, eine Gleichgewichtsgleichung und das ionische Produkt des Wassers)
b) Zeigen Sie, dass die Auflösung dieses Systems zu folgender Gleichung führt:
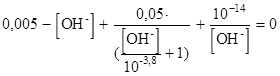Da wir uns in einer stark basischen Umgebung befinden, ist es besser, [OH-] als das Argument von f zu behalten, da die Werte von $ [H_3O^+] $ für die Maschinenberechnung zu niedrig sein können.
c) Lösen Sie diese Gleichung → hiermit.