Untersuchung des pH-Wertes während einer Titration einer starken Base durch eine starke Säure:

Anschließend bezeichnen wir durch $ x $ das Volumen (in $ mL $) von bereits hinzugefügtem $ HCl $ .

Anfangskonzentration der Base

$c_B$ = $\frac{c_{Α}V_{Α}}{V_B}$ = $\frac{0,05\cdot 0,040}{0,020}$ = $0,10 \frac{mol}{L}$

1.

pH zu Beginn der Titration   $(x=0)$

Die starke Base $ NaOH $ ist allein vorhanden, ihre Konzentration beträgt $c_B=0,10 \;M$ $pH=14+logc_B$ = $13$

2.

pH vor dem Equivalenzpunkt   ($x\;\lt\;40$)

(Der Einfachheit halber betrachten wir die Substanzen zuerst so, als wären sie nicht dissoziiert)

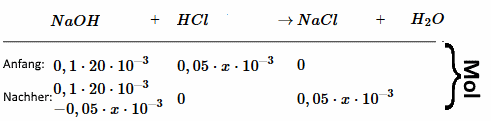
$c_{NaOH}$ = $\frac{n_{NaOH}}{(V_B+x)10^{-3}}$ = $\frac{0,1\cdot20\cdot10^{-3}-0,05\cdot x\cdot10^{-3}}{(20+x)10^{-3}}$ = $\frac{2-0,05\cdot x}{20+x}$ $pH$ $ =$ $ 14+log( \frac{2-0,05\cdot x}{20+x})$

3.

pH am Equivalenzpunkt   $(x\;=\;40)$

$HCl$ und $NaOH$ haben vollständig reagiert, bleibt eine neutrale Lösung von $NaCl$: $pH = 7$

4.

pH nach dem Equivalenzpunkt   $(x\;\gt\;40)$

$c_{HCl}$ = $\frac{n_{HCl}}{(V_B+x)10^{-3}}$ = $\frac{0,05\cdot x\cdot10^{-3}-0,1\cdot20\cdot10^{-3}}{(20+x)10^{-3}}$ = $\frac{0,05\cdot x-2}{20+x}$ $pH$ $=$ $ -log( \frac{0,05\cdot x-2}{20+x})$

→  Hier finden Sie Simulationen von solchen Titrationen