Bohrs Theorie hat es möglich gemacht, die Energieniveaus im H-Atom vollständig zu berechnen, aber leider gilt das nicht für komplexere Atome! Es war notwendig, etwas anderes zu finden, während die Grundidee der sowohl Wellen als auch Korpuskular-Natur des Lichts beibehalten wurde.
Albert Einstein fand heraus, dass es keinen fundamentalen Unterschied zwischen Materie und Energie gibt: Eine Masse $ m $ aus Materie und eine Menge an Energie $ E $ können gemäß folgender Formel ineinander umgewandelt werden:
$E$ $=$ $m\cdot c^2\;(1)$ wo $c$ $=$ $3\cdot 10^8 \frac{m}{s}$ die Lichtgeschwindigkeit ist und $ E $ die in Joule ausgedrückte Energie.
Also, $ 1 \; kg$ Materie kann theoretisch in eine phänomenale Energiemenge umgewandelt werden $1(3\cdot 10^8)^2$ $=$ $9\cdot10^{16}\; J$. Dies erklärt, warum bei Atombomben viel Energie aus wenig Materie freigesetzt werden kann!
Ein Photon mit einer Energie gleich $ E = h \nu $ wirkt (zum Beispiel während einer Kollision) so, als hätte es eine Masse von: $m$ $ =$ $ \frac{E}{c^2}$ $=$ $\frac{h\nu}{c^2}$ (2) $m$ heißt die "Ruhemasse" des Photons. Dies erklärt zum Beispiel, warum es durchaus möglich ist, $ \gamma $ -Photonen in Elektronen und Positronen umzuwandeln (Teilchen gleicher Masse wie Elektronen, aber mit positiver Ladung)
Den gesunden Menschenverstand völlig über Bord werfend, legte Louis de Broglie eine kühne Annahme vor: Da sich Photonen manchmal als Teilchen (Kollisionen), manchmal auch als Wellen (Beugung) verhalten, warum nicht in Betracht ziehen, dass alle Teilchen dasselbe tun könnten? Konkreter war De Broglie an einer Größe interessiert, die Physiker gut kennen, die bei elastischen Kollisionen erhalten bleibt: Der Impuls: $p$= $Masse\;\cdot\;Geschwindigkeit$. Gemäß der Formel (2) hängt der Impuls des Photons mit seiner Wellenlänge zusammen: $p_{photon}$ $=$ $mc$ $=$ $\frac{h\nu}{c}$ $=$ $\frac{h}{\lambda}$ (3) De Broglie dachte, dass der Impuls jedes Teilchens der Masse $ m $ und der Geschwindigkeit $ v $ mit der Wellenlänge dieses Teilchens (!!!) zusammenhängen würde:
$p_{particule}$ $=$ $m\;v$ $=$ $\frac{h}{\lambda}$ (4) Dabei ist $ m $ die Masse in $ kg $ des Teilchens und $ \lambda $ seine Wellenlänge ausgedrückt in $ m $.
Also würde sich ein Elektron der Masse $ m $ $ = $ $ 9,11 \cdot 10^{-31} kg $, das sich mit der Geschwindigkeit $ v $ $ = $ $ 10^6 \frac{m}{s} $ fortbewegt, ebenfalls verhalten wie eine Welle der Wellenlänge $\lambda$ $=$ $\frac{h}{mv}=$ $\frac{6,626\cdot 10^{-34}}{9,11\cdot10^{-31}\cdot 10^6}$ = $7,27\cdot 10^{-10}\;m$
De Broglie hatte recht gehabt:
- Wir können mit Elektronen Interferenzen produzieren!
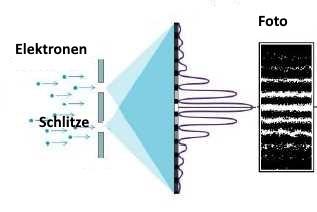- Ein einzelnes Elektron, das auf eine Wand mit zwei Schlitzen projiziert wird, durchläuft beide Schlitze (wie eine Welle!)
Erwin Schrödinger dachte über die mysteriöse Gleichung Bohrs nach, die so voraussehbar zu genauen Ergebnissen geführt hatte:
$ mvr $ $ = $ $ \frac{nh}{2 \pi} \; (5) $
Dabei ist $ m $ die Masse des Elektrons, $ v $ seine Geschwindigkeit in der Kreisbahn $ n $ des Wasserstoffatoms und $ r $ der Radius dieser Bahn.
Schrödinger versuchte diese Bedingung mit de Broglies Ideen zu verbinden:
Wenn $ \lambda $ die Wellenlänge des Elektrons ist, hätten wir laut de Broglie:
$mv$ $ =$ $ \frac{h}{\lambda}$ (4)
Wenn wir (4) und (5) kombinieren, würden wir finden:
$2\pi r$ $=$ $n\cdot \lambda\; (6)$
wo $2\pi r$ der Umfang der Bahn des Elektrons ist und $ \lambda $ seine Wellenlänge!
Bohrs Zustand würde also nichts weiter bedeuten, als dass die Wellenlänge des Elektrons eine ganze Anzahl von Malen im Umfang seiner Umlaufbahn enthalten sein sollte!
Solche Bedingungen waren beispielsweise in der Akustik bekannt.
(Wellenlänge des Schalls = Ganzzahlig in der Länge der Flöte enthaltenen !)
Die Elektronen der Atome unterliegen Resonanzbedingungen.