






Auf der Wasseroberfläche nähert sich eine progressive Welle einer Wand mit einem doppelten Schlitz. Hinter der Wand sieht man ein Interferenzphänomen. Es wird beobachtet, dass wenn man eine Linie parallel zur Wand führt dann wechseln sich hier die Maxima und Minima regelmäßig ab.

Ein Lichtstrahl von einem Laser wird mit einem Glasstab erweitert, dann auf eine Wand mit ein Doppelschlitz projiziert. Ein hinter der Wand platzierter Bildschirm sieht abwechselnd helle und dunkle Streifen erscheinen: Es ist ein Interferenzphänomen ähnlich wie oben beschrieben.

Licht ist ein Wellenphänomen
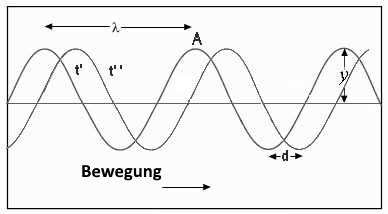
Die gezeigte Welle bewegt sich von links nach rechts. Sie wird zu Zeiten t' und t''mit t''> t' dargestellt. Während der Zeit t = t'' - t'hat sie die Strecke d zurückgelegt. Wir definieren:
Geschwindigkeit der Welle (Einheit: $1\frac{m}{s}$): $v$ $=$ $\frac{d}{t}\;(1)$ Wellenlänge (Einheit: $1\; m$): $\lambda$ = Abstand, der zwei aufeinander folgende Gipfel in einer bestimmten Zeit trennt
Ein Beobachter, der sich bei A befindet, sieht den Gipfel der Welle vorbeiziehen. Nach einer Zeit $ T $, sieht er den nächsten Gipfel vorbeiziehen. Die Welle legte dann die Entfernung $ \lambda $ zurück. Wir definieren:
Periode der Welle (Einheit: $1 \;s$): $T$ = Zeit, die ein Punkt der Welle braucht um die Entfernung $\lambda$ zurückzulegen.
Mit (1) erhalten wir die fundamentale Beziehung:
Grundlegende Beziehung: $v$ $=$ $\frac{\lambda}{T}\;(2)$
Ein in A lokalisierter Beobachter sieht $ \nu $ Scheitelpunkte der Welle in einer Sekunde vorüberziehen, das heißt, das Zeitintervall $ T $ ist $ \nu $ Mal in einer Sekunde enthalten. Wir definieren:
Frequenz der Welle (Einheit: 1 Hertz = $1 Hz$ = $1\; s^{-1})$: $\nu$ $=$ $\frac{1}{T}\;(3)$
$\nu$ ist die Häufigkeit, mit der ein Punkt der Welle in einer Sekunde den Abstand $ \lambda $ zurücklegt. Unter Verwendung von (2) und (3) reformulieren wir die fundamentale Beziehungen:
$v$ $=$ $\lambda \nu\;(4)$