





Ein Körper bewegt sich von A nach B unter dem Einfluss einer Kraft F, die einen Winkel α mit der Bahn macht. Die Kraft macht eine Arbeit $ W $
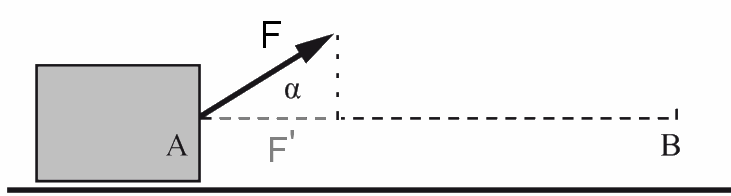
W = (Projektion von F auf AB) · AB W = F '& middot; AB
Die Kraft macht einen Winkel $ \alpha $ mit der Fortbewegung: Arbeit = $ W $ $ = $ $ F \cdot AB \cdot cos\alpha $
1 Joule = 1 Newton · 1 Meter $ 1 \; J $ $ = $ $ 1 \; N \cdot m $

$ W $ $ = $ $ F \cdot AB \cdot cos0^o $
Kraft parallel zur Fortbewegung und in selber Richtung: $ W $ $ = $ $ F \cdot AB $

$ W $ $ = $ $ F \cdot $ AB $ \cdot cos180 ^ o $
Kraft parallel zur Fortbewegung und in entgegengesetzter Richtung: $ W $ $ = $ $ -F \cdot AB $

$ W $ $ = $ $ F \cdot $ AB $ \cdot cos90^o $
Kraft senkrecht zur Verschiebung: $ W $ $ = $ $ 0 $

- Ein Skifahrer mit einem Gewicht von $ 650 \; N $ fährt einen Berg runter auf einer $ 2.000 \; m $ Piste, die einen $ 60 \;^o $ Winkel mit der Vertikalen macht. Berechnen Sie die Arbeit seines Gewichts. Antwort: $ W_P \; = \; 650 \cdot 2000 \cdot cos 60 \;^o $ $ = $ $ 650000 \; J $

- Ein Skifahrer mit einem Gewicht von $ 650 \; N $ verwendet einen Skilift, der einen Winkel von $ 110 \; ^o $ mit der Vertikalen über eine Länge von $ 2000 \; m $ macht. Berechnen Sie die Arbeit seines Gewichts. $W_P$ $=$ $650 \cdot 2000 \cdot cos 110\;^o$ $=$ $-444626 \;J $