Wärme erzeugt zwei wesentliche Effekte für die Materie, die sie empfängt oder verliert: - eine Variation der Temperatur, oder - eine Veränderung des physikalischen Zustands (fest, flüssig, gasförmig) der Materie.
"Wärmeleitung" ist der Transport von Wärme, die sich im Festkörper ausbreitet, wobei Metalle eine bessere Leitfähigkeit als Nichtmetalle haben. (Beispiel: der Metalllöffel in heißem Kaffee)
"Wärmestrahlung" ist ein Wärmetransport durch Infrarotstrahlen. (Bereich des elektromagnetischen Spektrums, der Wellenlängen größer als diejenigen des sichtbaren Lichts und niedriger als diejenigen von Mikrowellen entspricht). Alle Körper emittieren Wärmestrahlung, sofern sie eine Temperatur ungleich Null haben. (Beispiel: ein Ofen)
Die Wärme bewirkt, dass sich die Moleküle in einer Flüssigkeit im Allgemeinen von unten nach oben bewegen, da die heiße Flüssigkeit weniger dicht ist als die kalte Flüssigkeit. (Beispiel: Warmwasser-Zentralheizung)
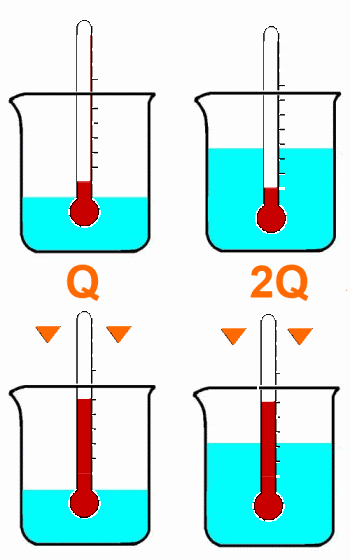
Es braucht doppelt so viel Wärme, um einen doppelten Temperaturanstieg zu erreichen:
Die Wärmemenge ist proportional zum Temperaturanstieg.
Es braucht doppelt so viel Wärme, um eine doppelte Masse zu erhitzen:
Die Wärmemenge ist proportional zur Masse.
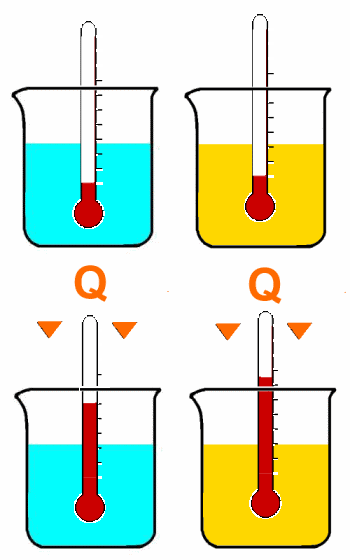Um unterschiedliche Materialien zu erhitzen, erzielen wir bei gleicher Wärmemenge einen unterschiedlichen Effekt:
Die Wärmemenge hängt vom Material ab.
$\Delta Q$ $ =$ $ c\;m\;\Delta T$ mit: $\Delta Q$ : Empfangene Wärmemenge $\Delta T$ : Temperaturvariation $m$ : Masse $c$ : Wärmekapazität (eine vom Material abhängige Konstante))
Die Kalorie ist die Wärmemenge, die benötigt wird, um die Temperatur von einem Gramm Wasser um $ 1 \; ^oC $ zu erhöhen
Durch die Einführung dieser Definition in die Grundformel ergibt sich: $\Delta Q$ $ =$ $ c\;m\;\Delta T$ $1\;cal$ $=$ $c\cdot 1\;g\cdot 1\;K$ $c$ $=$ $\frac{1\;cal }{1g\;1K}$ $c$ $=$ $1 \frac{cal}{g \cdot K}$
Wärmekapazität des Wassers: $c_{_{H_2O}}$ $=$ $1 \;\frac{cal}{g \cdot K}$
Ein Zuckerwürfel hat eine Masse von 3 g. Ein Gramm Zucker liefert bei Verbrennung $ 4\; kcal $. Wie viele Würfel sollten theoretisch brennen, um $ 600\;g$ Kaffee (selbes $ c $ wie Wasser) von $ 20^oC$ auf $ 100^oC$ zu erhitzen? Antwort: $\Delta Q$ $=$ $c\cdot m\Delta T $ $\Delta Q$ $=$ $1\cdot 600 \cdot (100-20)$ $=$ $48000\; cal$ $ =$ $48\; kcal$ Man muss also $\frac{48}{4}$ $=$ $12\;g$ Zucker verbrennen, d.h. $4$ Würfel!
