





Ein materielles System (zB eine sich bewegender Seilbahn) kann kinetischen Energie besitzen (z.B. aufgrund seiner Geschwindigkeit) und potentielle Energie (z.B. wegen seiner Höhe oder der Spannung des Kabels oder der Ladung einer Batterie) In der Chemie sind wir jedoch an Systemen interessiert, die aus einer Menge von Substanzen innerhalb des Behälters bestehen, in dem sie reagieren. Globale Faktoren wie die Geschwindigkeit, mit der sich der Container bewegt, oder die Höhe, in der er sich befindet, haben kein Interesse an der Charakterisierung dieser chemischen Systeme.
Das System besteht aus 2 Mol $ H_2 $ und 1 Mol $ O_2 $ in Standardbedingungen. In diesem Zustand kann viel mehr Arbeit in der äußeren Umgebung geleistet werden als in dem Zustand, in dem es sich zu zwei Mol Wasser verwandelt hat. (Der Beweis: Wasserstoffmotor!). Es muss daher Faktoren geben, die die innere Energie des Systems bestimmen.
Die innere Energie $ U $ eines chemischen Systems zu einem bestimmten Zeitpunkt wird bestimmt durch - die kinetische Energie aller chemischen Spezies, Moleküle, Atome oder Ionen, aus denen dieses System besteht - die potentielle Energie, die in den chemischen Bindungen enthalten ist. Betrachten Sie diese Verbindungen als Federn, in einigen Fällen "angespannter" als in anderen, also mehr energiehaltig!

Bewegung von Wassermolekülen
Es ist viel zu schwierig, die innere Energie U zu bewerten, wenn man einzeln die Bewegungen und Wechselwirkungen der großen Anzahl von Spezies betrachtet, aus denen die chemischen Systeme bestehen! Grundsätzlich muss aber die innere Energie U aus den Zustandsparametern $ P, V, T $ und $ n_i $ berechnet werden können. (Man sagt, dass U Zustandsfunktion ist). Da auch diese Berechnung in vielen konkreten Fällen sich zu kompliziert erwiesen hat, wird eher untersucht, wie U sich ändert, wenn ein System von einem Zustand in einen anderen übergeht . In der Tat kann jede vollständige chemische Reaktion als Übergang von einem System von einem Ausgangszustand (Reagenzien) zu einem Endzustand (den Produkten) betrachtet werden.
Physik lehrt uns, dass Wärme und Arbeit zwei "gleichwertige" Energieformen sind, das heißt, sie können gegenseitig umgewandelt werden . Deshalb werden sie in derselben Einheit ausgedrückt: $1\; Joule$ ($ J $) = $1\; Newton \cdot Meter$ ($ Nm $)
Energie muss global erhalten werden
Wenden wir dieses fundamentale Gesetz auf chemische Systeme an: Wenn ein System Energie gewinnt (also wenn seine innere Energie zunimmt), muss diese Energie von der äußeren Umgebung in Form von Wärme und / oder Arbeit kommen. Durch die Angabe von $ Q $ und $ W $ für die Wärme und Arbeit, die das System erhalten hat, haben wir:
$ \Delta U $ $ = $ $ Q $ $ + $ $ W $
Denken Sie daran, dass $ \Delta U $ bedeutet $ U_{Ende} $ $ - $ $ $ U_{Anfang} ist also der interne Energiegewinn . (Wenn $ \Delta U \lt 0 $, also die Ungleichung bedeutet, dass die innere Energie abnimmt, muss diese verlorene Energie in der äußeren Umgebung in Form von Wärme und / oder Arbeit wiederzufinden sein).
Da Wärme und Arbeit die durch ein chemisches System mit der Umgebung ausgetauscht werden leicht zu messen sind, so können wir experimentell die Änderung der inneren Energie während einer chemischen Transformation bestimmen!
Die Arbeit, die zwischen einem chemischen System und der äußeren Umgebung ausgetauscht wird, kommt in den meisten Fällen nur von Volumenschwankungen. Im Verbrennungsmotor eines Automobils sorgt die Gasexplosion (= das System) für Arbeit am Kolben und bewegt das Fahrzeug vorwärts (= die äußere Umgebung).
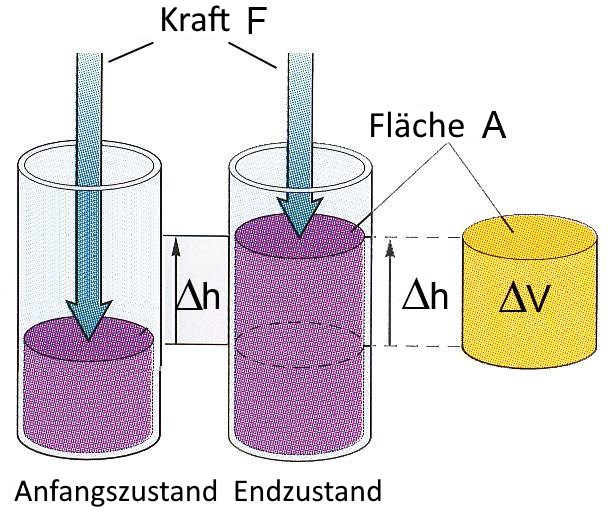
In den meisten chemischen Anwendungen geschehen Reaktionen unter konstantem Druck (oft der atmosphärische Druck): Nennen wir diesen Druck $ P $. Wenn der Druck P als $P$ = $\frac{F}{A} $ = definiert ist , entspannt sich das dargestellte Gas (System) also gegen die konstante Kraft $F$ $=$ $P\cdot A$ und liefert an die äussere Umbebung die Arbeit: $F\cdot\Delta h$ $=$ $P\cdot\Delta h\cdot A$ $=$ $P\cdot\Delta V$
Vom System empfangene Arbeit : $ W $ $ = $ $ -P \cdot \Delta V $
Messungen der Wärmemengen Austausch mit der Außenumgebung erfolgt im Kalorimeter :
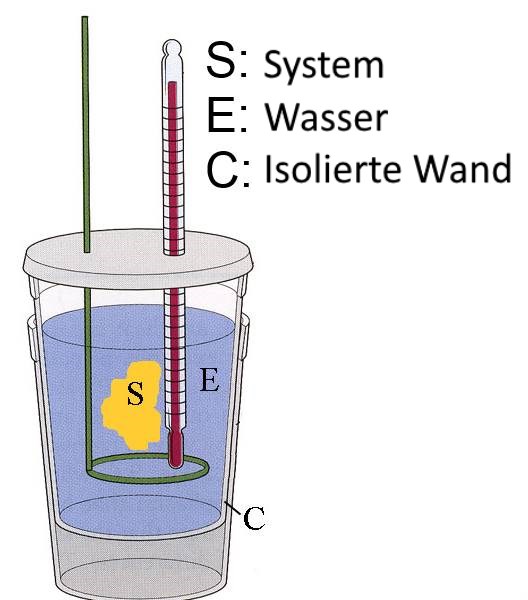
S: Das System, das von den reagierenden chemischen Spezies und ihren Produkten gebildet wird E: Wasser ist Teil der äußeren Umgebung, es empfängt eine Wärmemenge (in Joule) gleich $ 4184 \cdot m \cdot (\theta_f $ $ - $ $ \theta_i) $ wo $ 4184 \frac {J} {kg \cdot K} $ die spezifische Wärmekapazität des Wassers ist (= Anzahl der benötigten Joule um die Temperatur von einem Kilogramm Wasser um $1\;K$ zu erhöhen) $ m $ die Masse des Wassers ist(in Kilogramm), $ \theta_i $ die Temperatur zu Beginn der Reaktion ist und $ \theta_f $ die Temperatur am Ende der Reaktion ist (siehe Physik) C: Das Kalorimeter ist Teil der äußeren Umgebung, es empfängt eine Wärmemenge (in Joule) gleich $ C \cdot (\theta_f $ $ - $ $ \theta_i) $ wo $ C $ ist seine Wärmekapazität (in Joule pro $^oC$) ist.
Vom System empfangene Wärme : $ Q $ $ = $ $-4184 \cdot m \cdot (\theta_f $ $ - $ $ \theta_i) $ $ - $ C $ \cdot (\theta_f $ $ - $ $ \theta_i) $ wo: $ Q $ (in Joule) die Menge vom System an erhaltener Wärme ist, $ m $ (in Kilogramm) die Masse des Wassers ist, $ C $ (in Joule pro Grad) die Wärmekapazität des Kalorimeters ist. $ \theta_i, \theta_f $ die endgültigen Anfangs- und Endtemperaturen sind ,
$0,625\; g$ Formaldehyd ($ H_2CO $) werden beispielsweise in einem offenen Kalorimeter verbrannt: $ H_2CO $ $ + $ $ O_2 $ $ \longrightarrow $ $ CO_2 $ $ + $ $ H_2O $ Die Temperatur des Wasserbades ($150 g\; H_20$) steigt von $ 24,0^oC $ bis $ 39,2 \;^oC $. Die Wärmekapazität des Kalorimeters beträgt $ 150 \frac{J}{K} $: $ Q $ $ $ $ = -4184 \cdot 0.150 \cdot 15,2 $ $ - $ 150 $ \cdot 15,2$ $ \approx$ $-11820 J$
Die Kalorie ist eine alte Einheit für die Wärmemenge.
Eine Kalorie ($1\; cal$) ist die erforderliche Wärmemenge , um die Temperatur von 1 Gramm Wasser ein Grad zu erhöhen
Wenn wir in Gleichung (2) eingeben und den zweiten Term beiseite lassen, finden wir: $1 cal$ $=$ $4184\cdot 0,001\cdot 1$ $=$ $4,184 J$
$1\; cal$ $=$ $4,184\; J$ $1\; Joule$ $=$ $0,239 \;cal$
Chemiker bevorzugen (noch) oft die Kalorien für die Einheit der Wärmemenge und das Gramm für die Einheit der Masse. Gleichung (3) wird in diesem Fall:
Wärme erhalten vom System: $Q$ $=$ $- 1\cdot m \cdot (\theta_f$ $-$ $\theta_i)$ $-$ $C\cdot (\theta_f$ $-$ $\theta_i)$ wo: $ 1 \frac{cal}{g \ cdot K} $ die spezifische Wärmekapazität von Wasser ist, $ Q $ in $ cal $ ausgedrückt wird , $ m $ in $g$ $ C $ in $ \frac{cal}{K} $
Wenn wir veranlassen, dass der vom System erhaltene $ W $ -Auftrag in Gleichung (2) annulliert wird, dann folgt: $ \Delta U $ $ = $ $ Q $ , Die Variation der inneren Energie wird einfach die Wärme sein, die das System durch Kalorimetrie erhält! Dazu,um Volumenänderungen zu vermeiden, die durch das System in der Chemie allein verantwortlich für die ausgetauschte Arbeit sind, heißt es bei konstantem Volumen in einem hermetisch verschlossenen Kalorimeter ( "= Kalorimeterbombe") zu arbeiten
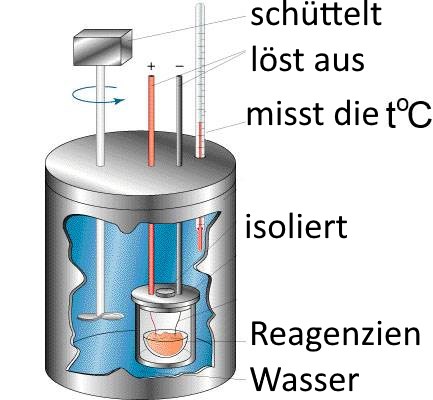
In einem geschlossenen Kalorimeter (bei konstantem Volumen): Variation der inneren Energie des Systems: $ \Delta U $ $ = $ $ Q $ = vom System empfangene Hitze