





Ein Dieselmotor liefert nur 45% der Leistung, die er zur Verfügung stellen könnte, wenn die gesamte Energie, die durch die Verbrennung des Diesels bereitgestellt wird, vollständig in Energie umgewandelt würde, die von dem Motor genutzt werden könnte. Die Verluste sind auf mehrfache und weitgehend unvermeidbare Ursachen zurückzuführen.


Um einen Apfelkuchen zu machen, braucht man 3 Äpfel, 2 Eier und genug Mehl.
 Wehe!
Diesmal waren drei Äpfel faul und aus 12 Äpfeln haben wir nur 3 Kuchen gemacht, während es 4 gewesen wären!
Die Ausbeute im Vergleich zu den Äpfeln ist
$\rho$ $=$ $\frac{3}{4}$ $=$
$0,75$
oder aber
$\rho$ $=$ $75\%$
(von den $100\%$ die man hätte kriegen können).
Wehe!
Diesmal waren drei Äpfel faul und aus 12 Äpfeln haben wir nur 3 Kuchen gemacht, während es 4 gewesen wären!
Die Ausbeute im Vergleich zu den Äpfeln ist
$\rho$ $=$ $\frac{3}{4}$ $=$
$0,75$
oder aber
$\rho$ $=$ $75\%$
(von den $100\%$ die man hätte kriegen können).
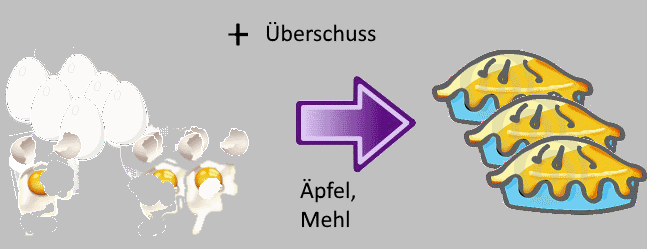 Wehe!
Diesmal waren drei Eier gebrochen und aus 9 Eiern haben wir nur 3 Kuchen gemacht, während es $ \frac{9}{2} $ hätten sein sollen!
Der Ausbeute in Bezug auf die Eier ist
$\rho$ $=$ $\frac{3}{\frac{9}{2}}$ $=$
$0,666$
oder aber
$\rho$ $=$ $66,6\%$
(von den $100\%$ die man hätte kriegen können).
Wehe!
Diesmal waren drei Eier gebrochen und aus 9 Eiern haben wir nur 3 Kuchen gemacht, während es $ \frac{9}{2} $ hätten sein sollen!
Der Ausbeute in Bezug auf die Eier ist
$\rho$ $=$ $\frac{3}{\frac{9}{2}}$ $=$
$0,666$
oder aber
$\rho$ $=$ $66,6\%$
(von den $100\%$ die man hätte kriegen können).
Die Ausbeute einer chemischen Reaktion ist das Verhältnis zwischen der Anzahl der Mole eines tatsächlich erhaltenen Produkts und der Anzahl der Mole dieses Produkts die theoretisch erhalten werden können. $\rho$ $=$ $\frac{n_{effectiv}}{n_{theoretisch}}$ Oft wird die Ausbeute in% ausgedrückt, also wird $ \rho $ mit 100 multipliziert : $\rho_{\%}$=$\frac{n_{effectiv}\cdot 100}{n_{theoretisch}}$

Hier sollten 3 Moleküle $ H_2 $ 3 Moleküle $ H_2O $ liefern, aber nur 2 (Verluste bei der Wasserrückgewinnung, fehlende Dichtheit der Behälter, u ...) Die Ausbeute bezogen auf das Wasserprodukt ist $\rho$ $=$ $\frac{2}{3}$ $=$ $0,666$ ou encore $\rho$ $=$ $66,6\%$
.