Ionengitter

Gitter vom Typ $ AB $

Dies sind Gitter, in denen positive Ionen A und negative Ionen B in gleicher Anzahl vorliegen. Die relative Größe der Ionen bestimmt den Gittertyp: Wenn positive und negative Ionen ungefähr die gleiche Größe haben , ist das Gitter häufig vom Caesiumchlorid-Typ $(Cs^+Cl^-)$ 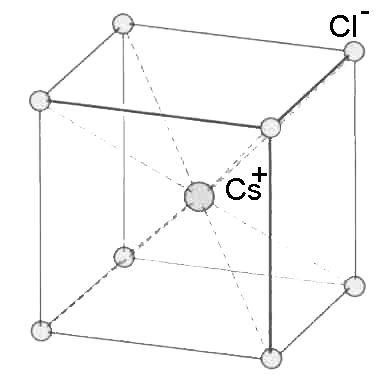Wenn der Durchmesser der Kationen etwa halb so groß ist wie der Durchmesser der Anionen, ist das Gitter häufig vom Natriumchlorid-Typ $(Na^+Cl^-)$ Wenn der Durchmesser der Kationen etwa ein Viertel des Durchmessers der Anionen beträgt, ist das Gitter häufig vom Sphalerit-Typ $(Zn^{2+}S^{2-})$ (Zinksulfid, Zinkblende)

Gitter vom Typ $ AB_2 $

Dies sind Gitter, in denen doppelt so viele Anionen B wie Kationen A vorhanden sind. Die relative Größe der Ionen bestimmt den Gittertyp: Wenn positive und negative Ionen ungefähr die gleiche Größe haben , ist das Gitter häufig vom Fluorit-Typ $(Ca^{2+}(F^-)_2)$ (Flussspat, Calciumfluorid) Wenn der Durchmesser der Kationen etwa halb so groß ist wie der Durchmesser der Anionen , ist das Gitter häufig vom Rutiltyp $(Ti^{4+}(O^{2-})_2)$ (Titan(IV) -oxid)

Die Einheitszelle

Die Einheitszelle ist die kleinste Struktur eines Gitters, die sich durch Translation durch den Kristall wiederholt.

Einheitszelle von Cäsiumchlorid

Die Zelle enthält $ 1 $ Kation (in der Mitte) und $ 8 \cdot \frac{1}{8} $ = $ 1 $ Anion. Die Ionen befinden sich auf der Diagonale $ d $ der Zelle und nicht auf einer Kante $ a $. Deshalb: $ d $ = Durchmesser des Anions + Durchmesser des Kations $ d = a\sqrt{3} $ Volumen der Zelle = $V$ $=$ $a^3$

Einheitszelle von Natriumchlorid

Die Zelle enthält $ 1 $ Kation (in der Mitte), $ 6 \cdot \frac{1}{2} $ = $ 3 $ Anionen in der Mitte der Seiten, $ 8 \cdot \frac{1}{8} $ $ = $ $ 1 $ Anion an den Ecken und $ 12 \cdot \frac{1}{4} = 3 $ Kationen in der Mitte der Kanten. Die Ionen berühren sich nur an der Kante $ a $ und nicht an der Diagonale $ d $. Deshalb: $ a $ = Durchmesser des Anions + Durchmesser des Kations $ d $ = $ a \sqrt{3} $ Volumen der Zelle = $V$ $=$ $a^3$

Die Elementarzelle bestimmt oft die makroskopische Kristallstruktur, aber nicht immer. Kristallographie untersucht die Geometrie von Kristallen.