





Ein heterogenes Gleichgewicht ist ein chemisches Gleichgewicht zwischen Substanzen, die in den verschiedenen Phasen sind, wobei mindestens einer dieser Stoffe in einer Phase ist, wo seine Konzentration konstant ist.
Angenommen, das Reagenz $ Y $ befindet sich in der Festphase, das Reagenz $ X $ und die Produkte $ C $ und $ D $ in der Gasphase: $aX_{(g)}$ $+$ $b$ $Y_{(s)}$$ \leftrightarrows$ $cC_{(g)}$ $+$ $dD_{(g)} $ (1) Es kann angenommen werden, dass die Reaktion nur dann möglich ist, wenn $ Y $ zuerst aus der festen Phase extrahiert wird, um in die gasförmige Phase überzugehen: $Y_{(s)}$$\leftrightarrows$$Y_{(g)}$ (2) Wir haben einem homogenes Gleichgewicht (1) und einem heterogenes Gleichgewicht (2)
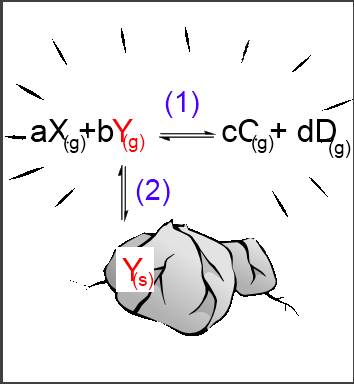
Wenden Sie die Gleichgewichtsgesetze für diese beiden Fälle an (1):$\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a\cdot[Y_{(g)}]^b}$ $=$ $K_c $ (2):$[Y_{(g)}]$ $=$ $K_{sat} $ (2) dans (1) : $\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a\cdot K_{sat}^b}$ $=$ $K_c $ $\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a}$ $=$ $K_c\cdot K_{sat}^b $ $ K_c\cdot K_{sat}^b$ ist eine neue Konstante, die wir mit $ K $ bezeichnen werden, Dabei gilt:
Für ein heterogenes Gleichgewicht $aX_{(g)}+b$ $Y_{(s)}$$ \leftrightarrows$ $cC_{(g)}$ $+$ $dD_{(g)} $, hat man: $\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a}$ $=$ $K $ Nach dem Gesetz von Gulberg und Waage kann man die chemische Spezies, die sich in der Phase befindet, in der ihre Konzentration konstant ist, weglassen.