






In diesem Experiment nimmt die Farbe (daher die Konzentration !) eines Reagens mit der Zeit ab. In der Physik definieren wir die Geschwindigkeit eines Autos als das Verhältnis zwischen der zurückgelegten Entfernung (= Variation der Entfernung ) und der Zeit, die notwendig ist, um diese Distanz zurückzulegen (= Variation der Zeit ). Analog dazu kommt in der Chemie die Idee, die Geschwindigkeit einer Reaktion zu definieren als Verhältnis zwischen der Konzentrationsvariation und der Dauer dieser Variation (= Variation der Zeit ).
Wenn $ \Delta [X] $ die Variation der Molarität eines Reagens X ist (= Endmolarität - Anfangsmolarität !), (= ein negativer Wert (die Molarität des Reagens X nimmt ab!), und $ \Delta t $ die Dauer dieser Variation, dann definieren wir:
Geschwindigkeit einer chemischen Reaktion bezüglich eines Reagens X : $v_X$ $=$ $\frac{\Delta[X]}{\Delta t}$
(Das Zeichen - kommt von der Tatsache, dass wir gerne eine positive Geschwindigkeit haben möchten!)
Wenn wir die Geschwindigkeit in Bezug auf ein Produkt Y der Reaktion definieren würden, müssten wir dieses Zeichen natürlich beiseite lassen, da die Molarität des Produktes mit der Zeit zunehmen würde!
Geschwindigkeit einer chemischen Reaktion bezüglich eines Produktes Y : $v_Y$ $=$ $\frac{\Delta[Y]}{\Delta t}$
Die bisher definierte Geschwindigkeit ist die Durchschnittsgeschwindigkeit der Reaktion zwischen zwei Zeiten $ t_i $ (Anfangszeit) und $ t_f $ (Endzeit) mit $\Delta t=t_f-t_i$.
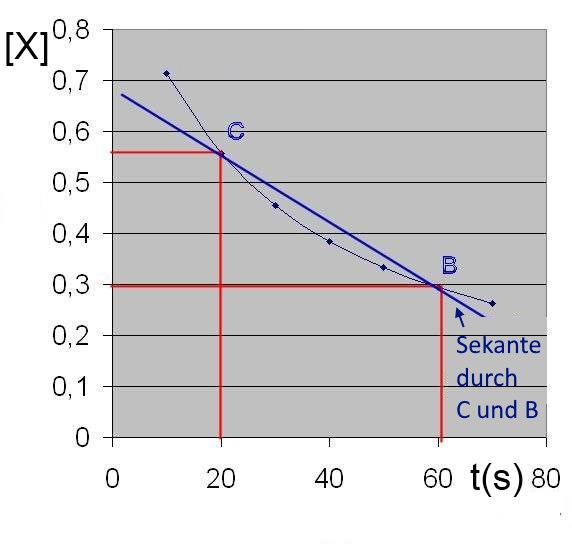
Durchschnittsgeschwindigkeit zwischen C und B = $-\frac{[X_f]-[X_i]}{t_f-t_i}$ = - Hang (Tangens) der Sekante durch C und B
( in diesem Fall ) = $-\frac{0,3-0,56}{60-20}$ = $0,0065$ $\frac{mol}{L\cdot s}$
Wenn wir diese Differenz sehr klein machen, erhalten wir eine Sofortgeschwindigkeit.
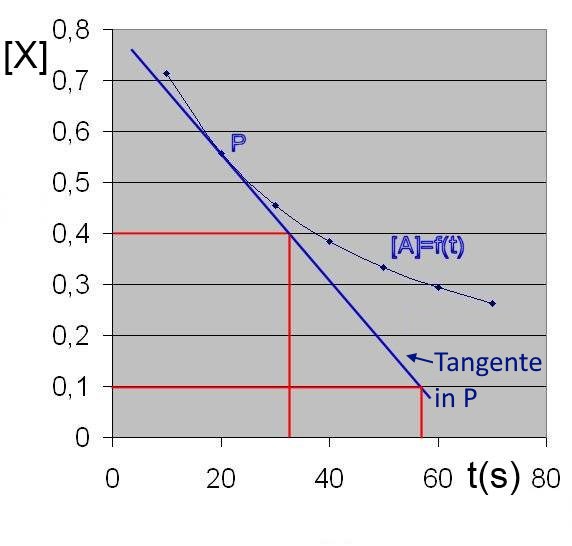
Sofortgeschwindigkeit im Punkt P = - Hang (Tangens) der Tangente in P
( in diesem Fall ) = $-\frac{0,1-0,4}{56-32}$ = $0,0125$ $\frac{mol}{L\cdot s}$