





Vodka ist eine Mischung aus Alkohol und Wasser.

Wasser ist das Lösungsmittel Alkohol ist der gelöste Stoff, (wir kürzen künftig ab mit: $so$) Vodka ist die Lösung, (wir kürzen künftig ab mit: $S$)
Die (Massen)dichte der Lösung ist das Verhältnis der Masse der Lösung zu ihrem Volumen:
(Massen)dichte der Lösung: $\rho_S$=$\frac{m_S}{V_S}$
Zum Beispiel, $\rho_{S}$ $=$ $0,95\frac{g}{cm^{3}}$ bedeutet, dass 1 $ cm^3 $ der $ S $ -Lösung eine Masse von $ 0,9 g $ hat In der Tat haben wir in diesem Fall: $\rho_{S}$ $=$ $\frac{0,95}{1}$ $=$ $0,95\frac{g}{cm^{3}}$
Die Anzahl der Mole des gelösten Stoffes ist das Verhältnis der Masse des gelösten Stoffes zu seiner Molmasse.
Anzahl der Mole des gelösten Stoffes : $n_{so}$ $=$ $\frac{m_{so}}{M_{so}}$
Zum Beispiel, $18 g$ Glucose $(C_6H_{12}O_6)$ sind $n_{glucose}$ $=$ $\frac{18}{6\cdot 12+12\cdot 1+ 6\cdot 16}$ $=$ $0,1 $ Mol
Der Prozentsatz des gelösten Stoffes ist das Verhältnis der Masse des gelösten Stoffes zur Masse der Lösung, dann multipliziert mit $ 100 $
Prozentsatz des gelösten Stoffes $\%_{so}$ $=$ $\frac{m_{so}\cdot 100}{m_S}$
Zum Beispiel, $\%_{so}$ $=$ $24$ bedeutet daß $100 g$ der Lösung $S$ enthalten $24 g$ des gelösten Stoffes $so$ In diesem Fall haben wir tatsächlich: $\%_{so}$=$\frac{24\cdot 100}{100}=24$
Die Molarität des gelösten Stoffes ist das Verhältnis der Molzahl des gelösten Stoffes zum Volumen der Lösung.
Molarität des gelösten Stoffes: $[so]$ $=$ $\frac{n_{so}}{V_S}$
Zum Beispiel, $[so]$ $=$ $2\frac{mol}{L}$ $=$ $2M$ (nicht zu verwechseln mit Molmasse M !) bedeutet, daß $ 1 L $ der $ S $ -Lösung 2 Mol des gelösten Stoffes $ so $ enthält In der Tat haben wir in diesem Fall: $[so]$ $=$ $\frac{2}{1}$ $=$ $2\frac{mol}{L}$
Jedes farbige Dreieck entspricht einer der vorangehenden Formeln:
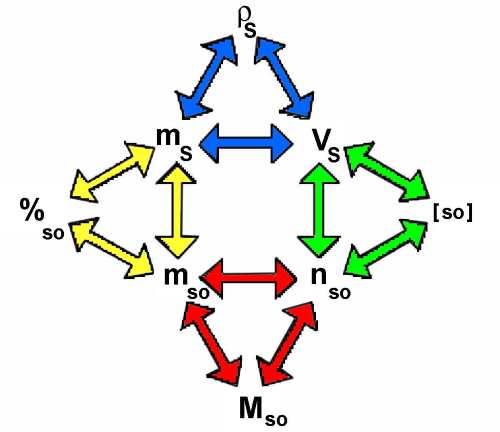
In jedem Dreieck kann eine Größe berechnet werden, wenn wir die anderen zwei kennen. Das Diagramm erlaubt, von einem Dreieck zum anderen überzugehen.
Beispiel:
$ 3 \; L $ einer Lösung mit Dichte $\rho_{S}$ $=$ $1,2\frac{g}{cm^3}$ enthalten $2\; mol$ eines gelösten Stoffes mit molarer Masse gleich $M_{so}$ $=$ $72\frac{g}{mol}$. Berechnen Sie den Prozentsatz des gelösten Stoffes in dieser Lösung!
Antwort:
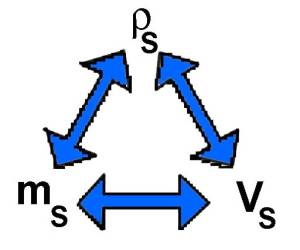
$3L$ $=$ $3000cm^3$ $\rho_S$=$\frac{m_S}{V_S}$ $ m_S$ $=$ $\rho_S\cdot V_S$ $m_S$ $=$ $1,2\cdot 3000$ $=$ $3600 g$
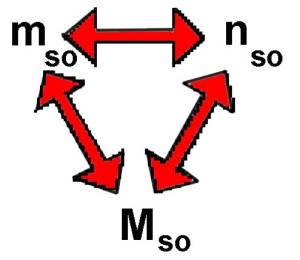
$n_{so}$ $=$ $\frac{m_{so}}{M_{so}}$ $m_{so}$ $=$ $n_{so}\cdot M_{so}$ $m_{so}$ $=$ $2\cdot 72$ $=$ $144 g$
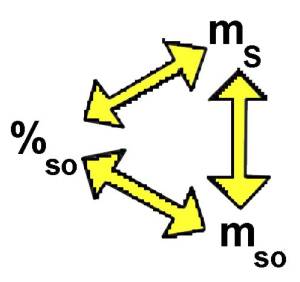
$\%_{so}$ $=$ $\frac{m_{so}\cdot 100}{m_S}$ $\%_{so}$ $=$ $\frac{144\cdot 100}{3600}$ $=$ $4$ Die Lösung enthält $4\%$ des gelösten Stoffes.