





(Betrifft Volumen - und Druckschwankungen bei einer Umwandlung einer festen Gasmenge bei konstanter Temperatur).
Der Kolben ermöglicht es, das Volumen zu variieren, das Manometer misst den Druck:

Resultate:
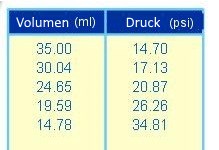
Indem wir den Druck mit dem Volumen multiplizieren, finden wir immer das gleiche Ergebnis!!
$P \cdot V = k_1$ wo $k_1$ eine Konstante bei gegebener Temperatur ist.
Mit anderen Worten, für das gleiche Gas bei einer gegebenen Temperatur, ausgehend von einem Zustand 1 (Druck $ P_1 $, Volumen $ V_1 $) bis zum Zustand 2 (Druck $ P_2 $, Volumen $ V_2 $), haben wir :
Bei konstanter Temperatur: $P_1 \cdot V_1$ $=$ $P_2 \cdot V_2$ ( = $k_1$)
(Betrifft die Variationen von Volumen und Temperatur während einer Umwandlung einer festen Menge von Gas bei konstantem Druck).
Die Heizung erlaubt das Volumen zu variieren, ein internes Thermometer misst die Temperatur:
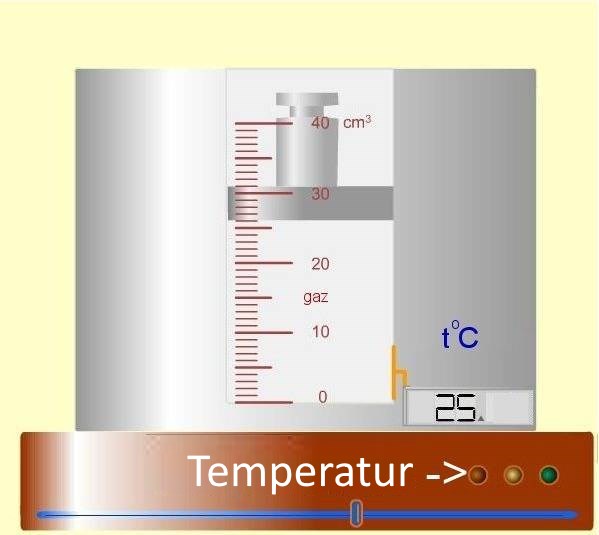
Resultate:
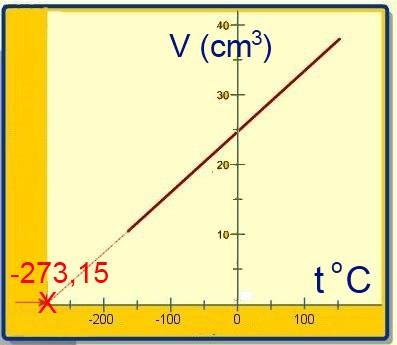
Die Funktion V = f(t) ist eine Gerade, welche die Temperaturachse auf der Abszisse $-273,15^oC $ schneidet.
Wenn wir eine neue Temperaturskala definieren durch:
Absolute Temperatur = Kelvin Temperatur = $T$ $=$ $273,15$ $+$ $t(^oC)$
dann liegt der Ursprung dieser Skala $ T = 0\; K $ bei $ -273,15^oC $ und der Graph V = g(T) ist der einer Geraden, die durch den Ursprung verläuft:

$V = k_2T$ wo $k_2$ eine konstante Zahl bei einem gegebenen Druck ist
Mit anderen Worten, für das gleiche Gas bei gegebenem Druck, ausgehend von einem Zustand 1 (absolute Temperatur $ T_1 $, Volumen $ V_1 $) in einen Zustand 2 (absolute Temperatur $ T_2 $, Volumen $ V_2 $), haben wir :
Bei konstantem Druck: $\frac{V_1}{T_1}$ $=$ $\frac{V_2}{T_2}$ ( = $k_2$)
(Betrifft Variationen in Volumen, Druck und Temperatur während einer Transformation einer festen Gasmenge) .
Betrachte die Umwandlung eines Gases von einem Zustand 1 in einen Zustand 2:
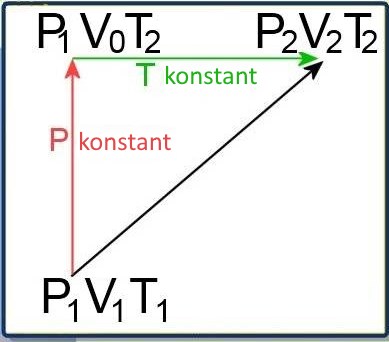
Seien $P_1$ , $V_1$ et $T_1$ Druck, Volumen und Temperatur im Zustand 1. Sind $ P_2 $, $ V_2 $ und $ T_2 $ Druck, Volumen und Temperatur im Zustand 2. Der Übergang von 1 nach 2 kann auch durch einen Umweg erfolgen, der aus einer Umwandlung bei konstantem Druck (a) gefolgt von einer Umwandlung bei konstanter Temperatur (b) besteht. (a)$\frac{V_1}{T_1}$ $=$ $\frac{V_0}{T_2}$ (Gay-Lussac) (b)$P_1\cdot V_0$ $=$ $P_2\cdot V_2$ (Boyle und Mariotte) Wenn wir $ V_0 $ zwischen (a) und (b) eliminieren, finden wir:
$\frac{P_1\cdot V_1}{T_1}=\frac{P_2\cdot V_2}{T_2}$
( Betrifft die Beschreibung des Zustandes eines Gases: Volumen, Druck, Temperatur und Anzahl der Mole)
.Lasst uns ein Mol Gas betrachten. Das vorherige Gesetz gilt: $\frac{P_1\cdot V_1}{T_1}$ $=$ $\frac{P_2\cdot V_2}{T_2}$ Also für jede Temperatur und Druck und für ein Mol von Gas bleibt $ \frac{P\cdot V} {T} $ konstant: $\frac{P\cdot V}{T}$ $=$ $R$ $V$ $=$ $R\frac{T}{P}$ wo $R$ eine Konstante ist für ein Mol Gas, Konstante die nicht mehr von Druck oder Temperatur abhängt. $R$ $=$ $0,082\frac{l\cdot atm}{mol\cdot K}$ wenn $P$ in atm und $V$ in L ausgedrückt wird. $R$ $=$ $8,3\frac{N\cdot m}{mol\cdot K}$ wenn $P$ in Pascal ($\frac{N}{m^2}$) und $V$ in $m^3$ ausgedrückt wird. Für n Mol Gas jedoch, unter den gleichen Bedingungen von Druck und Temperatur, nach dem Avogadro-Gesetz, wird das Volumen n mal größer sein: $V$=$n\cdot R\frac{T}{P}$ oder noch:
$P\cdot V$ $=$ $n\cdot R\cdot T$ mit $R$ $=$ $0,082\frac{l\cdot atm}{mol\cdot K}$ wenn $P$ in atm und $V$ in L ausgedrückt wird. $R$ $=$ $8,3\frac{N\cdot m}{mol\cdot K}$ wenn $P$ in Pascal ($\frac{N}{m^2}$) und $V$ in $m^3$ ausgedrückt wird.
(Betrifft das Volumen und die Anzahl der Mole eines Gases bei 0oC und 1 atm = normale Bedingungen von Temperatur und Druck STPD)
.Lassen Sie uns das Gesetz der idealen Gase anwenden (Form 2): $P\cdot V$ $=$ $n\cdot R\cdot T$ $1\cdot V$ $=$ $n\cdot 0,082\cdot 273,15$
Bei 0oC und 1 atm (STPD): $V$ $=$ $n\cdot 22,4$ wo $V$ in Liter ausgedrückt ist