La symétrie des molécules est essentielle en → stéréochimie La symétrie des réseaux est essentielle en cristallographie
Deux figures sont dites mutuellement symétriques si on peut les faire coïncider par une opération géométrique effectuée à l'aide d'opérateurs appelés éléments de symétrie:
|
|
|
|
| Point | I | Symétrie centrale |
| Plan | M encore désigné σ | Miroir |
| Axe de Rotation* | A2 encore désigné C2 ou 2 A3 encore désigné C3 ou3 A4 encore désigné C4 ou 4 A6 encore désigné C6 ou 6 |
Rotation de 180° Rotation de 120° Rotation de 90° Rotation de 60° |
* les axes de rotation-inversion sont caractérisées par la combinaison d'un axe et d'un centre de symétrie. les axes de rotation-réflexion sont caractérisées par la combinaison d'un axe et d'un plan de symétrie.
Exemples de centres de symétrie I
 Le cadre entier possède le centre de symétrie I: A' est l'image de A ,B' celle de B
Le cadre entier possède le centre de symétrie I: A' est l'image de A ,B' celle de B
 La molécule de cubane $C_8H_8$ possède le centre de symétrie I
La molécule de cubane $C_8H_8$ possède le centre de symétrie I
 Ce cristal de pyrite $FeS_2$ possède à l'intérieur le centre de symétrie I
Ce cristal de pyrite $FeS_2$ possède à l'intérieur le centre de symétrie I
Exemples de plans de symétrie M (encore désigné σ)
 La grenouille possède le plan de symétrie M (encore désigné σ): A' est l'image de A ,B' celle de B,C' celle de C
La grenouille possède le plan de symétrie M (encore désigné σ): A' est l'image de A ,B' celle de B,C' celle de C
 La molécule de formaldéhyde (méthanal) $CH_2O$ possède deux plans de symétrie M1 (encore désigné σ 1) et M2 (encore désigné σ 2).
La molécule de formaldéhyde (méthanal) $CH_2O$ possède deux plans de symétrie M1 (encore désigné σ 1) et M2 (encore désigné σ 2).
 Ce crystal de vivianite $Fe^{2+}_3(PO_4^{3-})_2·8H_2O$ possède le plan de symétrie M (encore désigné σ).
Ce crystal de vivianite $Fe^{2+}_3(PO_4^{3-})_2·8H_2O$ possède le plan de symétrie M (encore désigné σ).
Exemples d'axes de symétrie A2 encore désigné C2 ou 2 (encore désigné C2 ou 2)
 L'ancienne amphore possède quatre anses deux à deux opposées. Même si les anses ne sont pas tout à fait à angle droit, elle a un axe de symétrie d'ordre 2 A2 encore désigné C2 ou 2.
L'ancienne amphore possède quatre anses deux à deux opposées. Même si les anses ne sont pas tout à fait à angle droit, elle a un axe de symétrie d'ordre 2 A2 encore désigné C2 ou 2.
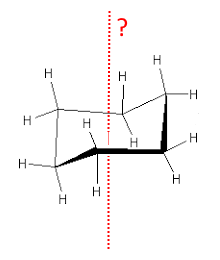
 Cette conformation bâteau du 1,3-dichlorocyclohexane a un axe de symétrie d'ordre 2 A2 encore désigné C2 ou 2: Tous les atomes se déduisent l'un de l'autre par une rotation de $180^o$ autour de cet axe.
Cette conformation bâteau du 1,3-dichlorocyclohexane a un axe de symétrie d'ordre 2 A2 encore désigné C2 ou 2: Tous les atomes se déduisent l'un de l'autre par une rotation de $180^o$ autour de cet axe.
 La sélénite $Ca^{2+}SO_4^{2-})·2H_2O$ a un axe de symétrie d'ordre 2: A2 encore désigné C2 ou 2.
La sélénite $Ca^{2+}SO_4^{2-})·2H_2O$ a un axe de symétrie d'ordre 2: A2 encore désigné C2 ou 2.
Exemples d'axes de symétrie A3 encore désigné C3 ou3
 Le tétraèdre de la plage de Pen-Bron possède a un axe de symétrie d'ordre 3 : A3 encore désigné C3 ou3.A' est l'image de A.
Le tétraèdre de la plage de Pen-Bron possède a un axe de symétrie d'ordre 3 : A3 encore désigné C3 ou3.A' est l'image de A.
 La molécule d'ammoniac $NH_3$ possède un axe de symétrie d'ordre 3: A3 encore désigné C3 ou3.
La molécule d'ammoniac $NH_3$ possède un axe de symétrie d'ordre 3: A3 encore désigné C3 ou3.
 Le quartz $SiO_2$ possède un axe de symétrie d'ordre 3 : A3 encore désigné C3 ou3.
Le quartz $SiO_2$ possède un axe de symétrie d'ordre 3 : A3 encore désigné C3 ou3.
>Exemples d'axes de symétrie A4 encore désigné C4 ou 4
 La pyramide de Khéops possède a un axe de symétrie d'ordre 4 : A4 encore désigné C4 ou 4.
La pyramide de Khéops possède a un axe de symétrie d'ordre 4 : A4 encore désigné C4 ou 4.
 La molécule de pentaborane(9) $B_5H_9$ possède un axe de symétrie d'ordre 4 : A4 encore désigné C4 ou 4.
La molécule de pentaborane(9) $B_5H_9$ possède un axe de symétrie d'ordre 4 : A4 encore désigné C4 ou 4.
 La cassitérite $SnO_2$ possède un axe de symétrie d'ordre 4 : A4 encore désigné C4 ou 4.
La cassitérite $SnO_2$ possède un axe de symétrie d'ordre 4 : A4 encore désigné C4 ou 4.
Exemples d'axes de symétrie A6 encore désigné C6 ou 6
 L'ancienne église Notre Dame de Nazareth possède a un axe de symétrie d'ordre 6 : A6 encore désigné C6 ou 6.
L'ancienne église Notre Dame de Nazareth possède a un axe de symétrie d'ordre 6 : A6 encore désigné C6 ou 6.
 La molécule de benzüne $C_6H_6$ possède un axe de symétrie d'ordre 6 : A6 encore désigné C6 ou 6.
La molécule de benzüne $C_6H_6$ possède un axe de symétrie d'ordre 6 : A6 encore désigné C6 ou 6.
 L'émeraude $Be_3(Al,M)_2(SiO_3)_6,\;(M \;= \;Cr, Fe, V)$ possède un axe de symétrie d'ordre 6 : A6 encore désigné C6 ou 6.
L'émeraude $Be_3(Al,M)_2(SiO_3)_6,\;(M \;= \;Cr, Fe, V)$ possède un axe de symétrie d'ordre 6 : A6 encore désigné C6 ou 6.
Les axes de rotation-inversion sont caractérisées par la combinaison d'un axe et d'un centre de symétrie.
 Le cube possède un axe de rotation-inversion d'ordre 3: : $\bar{A3}$ encore désigné $\bar{C3}$ ou $\bar{3}$: Le point $A$ donne par rotation de $120^o$ le point X (1), qui, à son tour, par symétrie centrale, donne le point image $A'$ (2).
Remarque:
La rotation-inversion d'ordre 1 est la composée d'une rotation d'angle 360° et d'une inversion,: $\bar{1}= \;i $ .
La rotation-inversion d'ordre 2 donnée en exemple est en fait une réflexion par rapport au plan miroir perpendiculaire à l'axe de rotation et passant par le centre d'inversion : $\bar{2}=\sigma $ .
Le cube possède un axe de rotation-inversion d'ordre 3: : $\bar{A3}$ encore désigné $\bar{C3}$ ou $\bar{3}$: Le point $A$ donne par rotation de $120^o$ le point X (1), qui, à son tour, par symétrie centrale, donne le point image $A'$ (2).
Remarque:
La rotation-inversion d'ordre 1 est la composée d'une rotation d'angle 360° et d'une inversion,: $\bar{1}= \;i $ .
La rotation-inversion d'ordre 2 donnée en exemple est en fait une réflexion par rapport au plan miroir perpendiculaire à l'axe de rotation et passant par le centre d'inversion : $\bar{2}=\sigma $ .

Les axes de rotation-réflexion sont caractérisées par la combinaison d'un axe et d'un plan de symétrie perpendiculaire à cet axe.
 Le tétraèdre possède un axe de rotation-réflexion d'ordre 4: : $S4$ : Le point $A$ donne par rotation de $90^o$ le point X (1), qui, à son tour, par réflexion sur le plan, donne le point image $A'$ (2).
Le tétraèdre possède un axe de rotation-réflexion d'ordre 4: : $S4$ : Le point $A$ donne par rotation de $90^o$ le point X (1), qui, à son tour, par réflexion sur le plan, donne le point image $A'$ (2).
Remarque: Comme le miroir (réflexion par rapport au plan) est équivalent à une rotation de π suivie d'une inversion, une rotation-reflexion ( par définition une rotation de θ suivie d'un miroir) est donc une rotation-inversion d'angle θ+π La rotation-réflexion d'ordre 1 est donc un miroir : $S1= \sigma $ . La rotation-réflexion d'ordre 2 est donc une inversion : $S2= \;i $ .
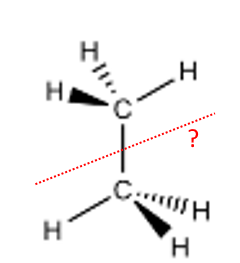
 Trouvez l'axe de rotation verticale ( cliquez )
Trouvez l'axe de rotation verticale ( cliquez )
 Trouvez le nombe de niroirs ( cliquez )
Trouvez le nombe de niroirs ( cliquez )
 Trouvez le nombe d'axes de rotation-réflexion ( cliquez )
Trouvez le nombe d'axes de rotation-réflexion ( cliquez )
Cliquez sur les figures suivantes pour identifier l'élément de symétrie représenté: