





Définition On appelle quantité de mouvement $p$ d'un corps le produit de sa masse par la vitesse:
Quantité de mouvement: $p$ $=$ $m\cdot \vec{v}$ avec: $m$ la masse $\vec{v}$ la vitesse
La loi fondamentale Utilisons une des → hypothèses initiales de la théorie cinétique des gaz: $\vec{F}=m\frac{\Delta \vec{v}}{\Delta t}$ $\vec{F}=\frac{\Delta m\vec{v}}{\Delta t}$
Force: $\vec{F}=\frac{\Delta \vec{p}}{\Delta t}$ La force est égale à la variation de la quantité de mouvement

Si le choc est élastique, la molécule possédant une vitesse $\vec{V}\binom{v_x}{v_y}$ rebondit avec une vitesse $\vec{V´}\binom{-v_x}{v_y}$ La variation de la quantité de mouvement vaut donc: $\Delta{p}$ = $\Delta m\vec{v}$ = $m\binom{-v_x}{v_y}-m\binom{v_x}{v_y}$ = $m\binom{-2v_x}{0}$

Notre gaz idéal est formé de molécules qui se meuvent sans interagir au hasard dans tous les sens dans une boîte de volume $V=A\cdot L$ Procédons par étapes pour évaluer la pression sur la paroi $A$:
Regardons une molécule: - Sa vitesse dans la direction $x$ vaut $v_x$ avant ou après son choc contre la paroi $A$ - Le temps entre deux chocs contre cette même paroi est donc le temps pour faire un aller-retour dans la boîte dans la direction $x$

- D'après la formule: temps = $\frac{distance}{vitesse}$ ce temps peut être évalué par: $\Delta t=\frac{2L}{v_x}$ L'intensité de la force que la paroi a exercé sur la molécule vaut donc: $f =$ $\frac{1}{\Delta t}2mv_x =$ $\frac{2mv_x}{\frac{2L}{v_x}} =$ $\frac{mv_x^2}{L}$ D'après la loi de l'action et de la réaction de Newton c'est aussi l'intensité de la force que la molécule a exercé sur la paroi!
Soient $1,2,3,4,5,..........N$ les molécules de la boîte. Alors la force sur la paroi $A$ vaut $F=$ $f_1+f_2+f_3+f_4+f_5+......f_N =$ $\frac{m[v_{1x}^2+v_{2x}^2+v_{3x}^2+v_{4x}^2+v_{5x}^2+......v_{Nx}^2]}{L}$ Désignons par $u_x^2$ la moyenne des carrés des composantes des vitesses sur la direction x, par $u_y^2$ la moyenne des carrés des composantes des vitesses sur la direction y, par $u_z^2$ la moyenne des carrés des composantes des vitesses sur la direction z, par $u^2$ la moyenne des carrés des vitesses réelles des molécules donc: $u_x^2 =$ $\frac{m[v_{1x}^2+v_{2x}^2+v_{3x}^2+v_{4x}^2+v_{5x}^2+......v_{Nx}^2]}{N}$ alors: $F=$ $\frac{mNu_x^2}{L}$ Comme nous avons supposé qu'il n'y a pas de direction priviligiée au déplacement des molécules dans le gaz, on peut dire que $u_x^2=u_y^2=u_z^2$
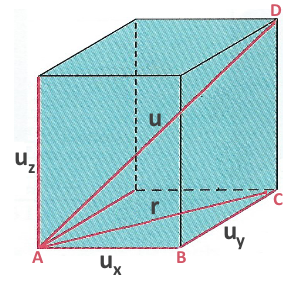
Employons le théorême de Pythagore pour les triangles ABC et ACD: $r^2$ $=$ $u_x^2+u_y^2$ $u^2$ $=$ $r^2+u_z^2$ $=$ $u_x^2+u_y^2+u_z^2=3u_x^2$ alors: $F=$ $\frac{mNu^2}{3L}$
En employant la définition de la pression: $P$ = $\frac{F}{A}$ nous trouvons $P$ = $\frac{\frac{mNu^2}{3L}}{A} =$ $\frac{mNu^2}{3L\cdot A} =$ $\frac{mNu^2}{3V}$
Pression du gaz: $P=\frac{mNu^2}{3V}$ où $V$ est le volume du gaz $m$ la masse d'une molécule $N$ le nombre de molécules