





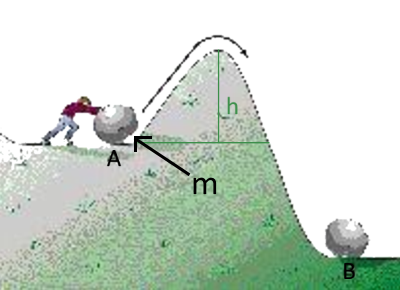
Rappel de physique: Pour pousser la balle de masse m de $A$ en $B$ , Paul doit faire un travail $W=9,8\;m\;h$ $m$ en $kg$ $h$ en mètres $W$ en Joule On pourrait dire que ce travail est l'énergie d'activation de la transformation $A\longrightarrow B$ Si Paul n'a pas cette énergie, la balle revient en $A$ !
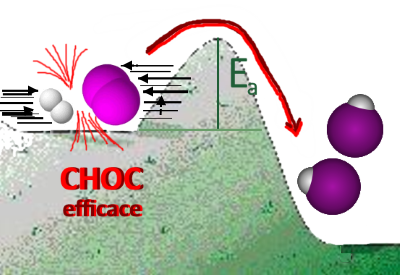
Si la vitesse des réactifs est suffisante (température assez élevée), elles pourront vaincre par leur choc la barrière constituée par la répulsion des noyaux (l'énergie d'activation) et se transformer en produits
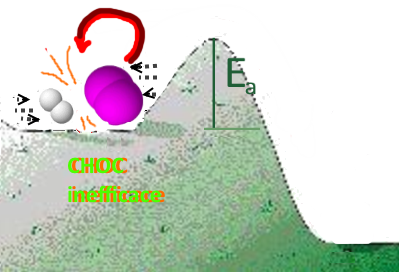
Si la vitesse des réactifs est insuffisante (température pas assez élevée) ou si l'énergie d'activation est trop élevée, cela n'est plus possible!

Svante Arrhénius (1859-1929)
Arrhénius a trouvé que la constante de vitesse se laisse exprimer de la manière suivante:
$k=Ae^{-\frac{E_a}{R\cdot T}}$
où - $T$ est la température absolue (en $K$) - $E_a$ l'énergie d'activation (en $J$ ) - $R$ la constante des gaz parfaits $(8,3 \frac{J}{mol\; K} )$ - A $\approx$ une constante pour une réaction donnée On voit que $k$ (et donc la vitesse de réaction) diminue quand - $E_a$ augmente (barrière plus élevée!) - $T$ diminue (moins de chocs et chocs moins forts)