





Inspiré par l'excellent → exposé du professeur Tuckerman
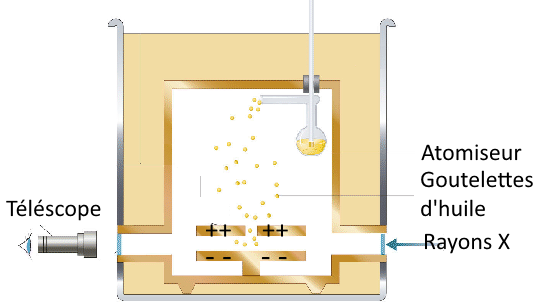
Des goutelettes d'huile de masse $M$ tombent dans un champ électrique $E$ . Quelques-unes restent en suspension entre les plaques. Ce sont (probablement) celles qui ont capté un électron par action des rayons X. Elles possèdent une charge élémentaire négative $e$ Leur poids doit être égal à la force électrique qui les retient! On a: $M\cdot g$ $=$ $e\cdot E$ $\frac{M}{e}$ $=$ $\frac{g}{E}$ (1)
Si y est fonction de x, l'équation différentielle $\frac{dy}{dx}$ $=$ $ay$ $+$ $b$ possède une solution: $y$ $=$ $e^{ax}$ $-$ $\frac{b}{a}$ (2) En effet, alors $\frac{dy}{dx}$ = $ae^{ax}$ = $a(y$ $+$ $\frac{b}{a})$ = $ay$ $+$ $b$

Les goutelettes d'huile tombent sans champ électrique. Alors deux forces s'exercent sur elles: 1) le poids $P$ $=$ $M\cdot g $ 2) la force de frottement $F$ $=$ $\gamma \cdot v $ où $\gamma $ est le coëfficient de friction La force résultante est donc: $P$ $-$ $F$ $=$ $M\cdot g$ $-$ $\gamma \cdot v$ D'après la loi de Newton, on a: $M\cdot \frac{dv}{dt}$ $=$ $M\cdot g$ $-$ $\gamma \cdot v$ $ \frac{dv}{dt}$ $=$ $g$ $-$ $\frac{\gamma}{M} \cdot v$ ce qui est une équation différentielle du type (2) avec $a$ $=$ $-\frac{\gamma}{M} $ et $b$ $=$ $g$ et qui possède donc la solution: $v$ $=$ $\frac{Mg}{\gamma}(1+e^{-\frac{\gamma \cdot t}{M}})$ Comme $\gamma$ est ssez grand et $M$ petit, le deuxième terme tend rapidement vers 0 et pour la vitesse stationnaire $V$ observée on a: $V$ $=$ $\frac{Mg}{\gamma}$ (3) Cette équation permet donc de déterminer $M$ et par (1) aussi $e$ ! On trouve:
$e$ $=$ $1,6\cdot 10^{-19}\;C$