Étude du pH au cours d'une titration d'un acide faible par une base forte

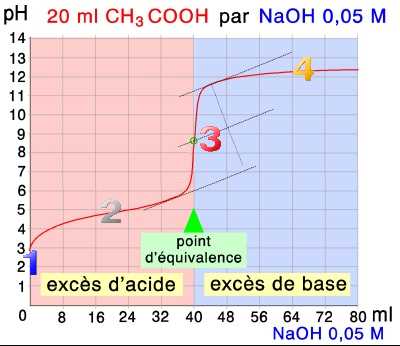
Par la suite nous désignons par $x$ le volume (en $mL$) de $NaOH$ déjà ajouté.

Concentration initiale de l'acide

$c_{Α}$ = $\frac{c_BV_B}{V_{Α}}$ = $\frac{0,05\cdot 0,040}{0,020}$ = $0,10 \frac{mol}{L}$

1.

pH au début de titration  ($x=0$)

L'acide faible $CH_3COOH$ est seul présent, sa concentration vaut $c_{Α}=0,10 \;M$ Acide faible! $pH=\frac{1}{2}pK_a-\frac{1}{2}logc_{Α}$ $=\frac{1}{2}4,75-\frac{1}{2}log0,1$ $pH\;=\;2,88$

2.

pH avant le point équivalent  ($x\;\lt\;40$)

(pour simplifier, nous considérons les substances d'abord comme si elles n'étaient pas dissociées)

Tampon! $pH$ = $pK_a$ $+$ $log( \frac{n_{CH_3COONa}}{n_{CH_3COOH}})$ = $4,75$ $+$ $log( \frac{0,05\cdot x\cdot10^{-3}}{0,1\cdot20\cdot 10^{-3}-0,05\cdot x\cdot10^{-3}})$ $pH$ $ =$ $ 4,75+log( \frac{0,05\cdot x\cdot}{0,1\cdot20-0,05\cdot x})$

3.

pH au point équivalent  ($x\;=\;40$)

$CH_3COOH$ et $NaOH$ ont réagi entièrement, reste une solution de la base faible $CH_3COO^-$ Base faible! $pH$ $ =$ $ 14$ $-$ $\frac{1}{2}pK_B$ $+$ $\frac{1}{2}log (c_{CH_3COONa})$ $ = $ $14$ $-$ $\frac{1}{2}9,25$ $+$ $\frac{1}{2}log (\frac{0,1\cdot20\cdot 10^{-3}}{(20+40)\cdot 10^{-3}})$ $pH = 8,63$

4.

pH après le point équivalent  ($x\;\gt\;40$)

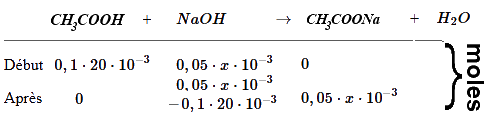
Base forte prime devant base faible! Base forte! $c_{NaOH}$ $= \frac{n_{NaOH}}{(V_{Α}+x)10^{-3}}$ $= \frac{0,05\cdot x\cdot10^{-3}-0,1\cdot20\cdot10^{-3}}{(20+x)10^{-3}}$ $= \frac{0,05\cdot x-2}{20+x}$ $pH$ $ =$ $ 14$ $+$ $log( \frac{0,05\cdot x-2}{20+x})$

→   Voici des simulations de ces titrations