Par sa dissociation,
$HB$ $+$ $H_2O$ $\rightleftarrows$ $ H_3O^+$ $+$ $B$
un acide, même faible, apporte en général beaucoup plus d'ions hydronium dans l'eau que l'autoprotolyse de l'eau elle-même.
Appelons $n_{HB}$ le nombre de moles d'acide $HB$ introduits dans l'eau avant qu'il ne se soit dissocié. Si $V$ est le volume final, sa molarité initiale (formelle) s'écrit:
$c_{HB}$ $=$ $\frac{n_{HB}}{V}$
Appelons $x$ le nombre de moles d'hydronium $H_3O^+$ présents dans la solution au moment où l'équilibre de dissociation est atteint.
Alors on a:
$H_3O^+$ $=$ $ \frac{x}{V}$
$pH$ $ =$ $ -log(\frac{x}{V})$
Déterminons $x$:
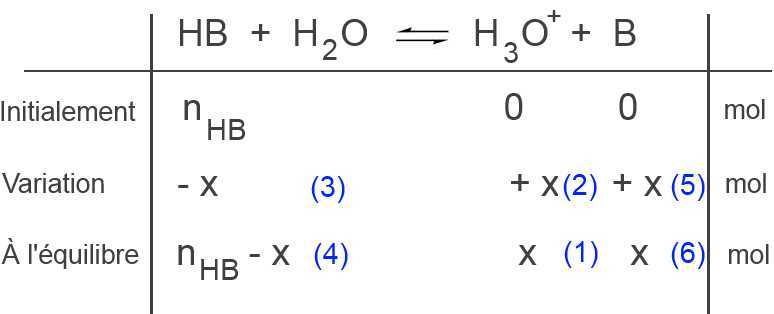Nous trouvons dans l'ordre:
(1) $x$ moles $H_3O^+$ à l'équilibre
(2) $x$ moles $H_3O^+$ produits
(3) $x$ moles $HB$ disparus
(4) $n_{HB}-x$ moles $HB$ à l'équilibre
(5) $x$ moles $B$ produits
(6) $x$ moles $B$ à l'équilibre
Les molarités à l'équilibre sont donc:
$[H_3O^+]$ $=$ $\frac{x}{V}$
$[HB]$ $=$ $\frac{n_{HB}-x}{V}$
$[B]$ $=$ $\frac{x}{V}$
Introduisons dans l'expression de la constante d'acidité $K_a$:
$K_a$ $=$ $\frac{[H_3O^+][B]}{[HB]}$ =
$\frac{\frac{x}{V}\frac{x}{V}}{\frac{n_{HB}-x}{V}}$ =
$\frac{\frac{x}{V}\frac{x}{V}}{\frac{n_{HB}}{V}-\frac{x}{V}}$ =
$\frac{[H_3O^+]^2}{c_{HB}-[H_3O^+]}$
$[H_3O^+]^2$ $+$ $K_a[H_3O^+]$ $-$ $K_ac_{HB}$ $=$ $0$
d'où en posant $y$ $=$ $[H_3O^+]$:
Calcul du $pH$ d'une solution diluée d'acide faible: 1) on cherche une solution raisonnable de l'équation: $y^2$ $+$ $K_a\cdot y$ $-$ $K_a c_{HB}$ $=$ $0$ 2) on calcule: $pH$ $=$ $-log\;y$
Par exemple: Soit une solution d'acide faible $0,10\frac{mol}{L}$ avec $K_a$ $=$ $4,00\cdot 10^{-2}$: L'équation $y^2$ $+$ $4,0\cdot10^{-2}\cdot y$ $-$ $4,0\cdot10^{-2}\cdot0,10$ $=$ $0$ fournit la racine positive: $y$ $=$ $8,3\;\cdot 10^{-3}$ et ainsi: $pH$ $=$ $-log\; y$ = $2,1$