La théorie de Bohr a permis de calculer entièrement les niveaux d'énergie dans l'atome H, mais elle ne s'applique malheureusement pas à des atomes plus complexes! Il fallait donc trouver autre chose tout en gardant l'idée fondamentale de la nature à la fois ondulatoire et corpusculaire de la lumière.
Albert Einstein a trouvé qu'il n'existe pas de différence fondamentale entre la matière et énergie: Une masse $m$ de matière et une quantité d'énergie $E$ peuvent être converties mutuellement l'une dans l'autre d'après la formule:
$E$ $=$ $m\cdot c^2\;(1)$ où $c$ $=$ $3\cdot 10^8 \frac{m}{s}$ est la vitesse de la lumière et $E$ l'énergie exprimée en Joule.
Ainsi, $1\; kg$ de matière peut théoriquement être convertie en une quantité d'énergie phénoménale de $1(3\cdot 10^8)^2$ $=$ $9\cdot10^{16}\; J$. Ceci explique pourquoi, dans les bombes atomiques, beaucoup d'énergie peut être libérée à partir de peu de matière!
Un photon transportant une énergie égale $E=h\nu$ agit (par exemple lors d'un choc) comme s'il avait une masse de: $m$ $ =$ $ \frac{E}{c^2}$ $=$ $\frac{h\nu}{c^2}$ (2) $m$ s'appelle la "masse au repos" du photon. Cela explique par exemple pourquoi il est parfaitement possible de transformer des photons $\gamma$ en électrons et positrons (particules de même masse que les électrons, mais de charge positive)
Jetant le sens commun entièrement par-dessus bord, Louis de Broglie présenta une hypothèse audacieuse: Puisque les photons se comportent tantôt comme particules (chocs), tantôt comme ondes (diffraction), pourquoi ne pas envisager que toutes les particules} ne puissent agir de même? Plus concrètement, de Broglie s'intéressa à une grandeur dont les physiciens savent bien qu'elle se conserve lors de chocs élastiques: La quantité de mouvement: $p$= $masse\;\cdot\;vitesse$. D'après la formule (2) la quantité de mouvement du photon est liée à sa longueur d'onde: $p_{photon}$ $=$ $mc$ $=$ $\frac{h\nu}{c}$ $=$ $\frac{h}{\lambda}$ (3) De Broglie envisagea que la quantité de mouvement de n'importe quelle particule de masse $m$ et évoluant avec la vitesse $v$ serait liée à la longueur d'onde de cette particule(!!!):
$p_{particule}$ $=$ $m\;v$ $=$ $\frac{h}{\lambda}$ (4) où $m$ est la masse en $kg$ de la particule et $\lambda$ sa longueur d'onde exprimée en $m$.
Ainsi, un électron de masse $m$ $=$ $9,11\cdot10^{-31}kg$ évoluant avec la vitesse $v$ $=$ $10^6\frac{m}{s}$ se comporterait aussi comme une onde de longueur d'onde $\lambda$ $=$ $\frac{h}{mv}=$ $\frac{6,626\cdot 10^{-34}}{9,11\cdot10^{-31}\cdot 10^6}$ = $7,27\cdot 10^{-10}\;m$
De Broglie avait vu juste:
- On peut faire des interférences avec des électrons !
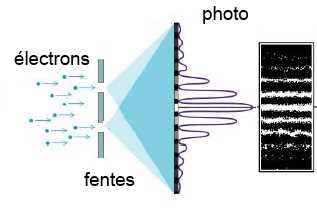- Un seul électron projeté sur une paroi avec deux fentes passe par les deux fentes (comme une onde!)
Erwin Schrödinger réfléchit à la mystérieuse condition de Bohr qui menait d'une manière si providentielle à des résultats exacts:
$mvr$ $=$ $\frac{nh}{2\pi}\;(5)$
où $m$ est la masse de l'électron, $v$ sa vitesse sur l'orbite circulaire $n$ de l'atome d'hydrogène et $r$ le rayon de cette orbite.
Schrödinger essaya de combiner cette condition avec les idées de de Broglie:
Si $\lambda$ est la longueur d'onde de l'électron, on aurait d'après de Broglie:
$mv$ $ =$ $ \frac{h}{\lambda}$ (4)
En combinant (4) et (5), on trouverait:
$2\pi r$ $=$ $n\cdot \lambda\; (6)$
où $2\pi r$ est la circonférence de l'orbite de l'électron et $\lambda $ sa longueur d'onde!
La condition de Bohr ne signifierait donc rien d'autre que la longueur d'onde de l'électron devrait être contenue un nombre entier de fois dans la circonférence de son orbite!
De telles conditions étaient bien connues par exemple en acoustique.
(Longueur d'onde du son = nombre entier de fois contenue dans la longueur de la flûte!)
Les électrons des atomes obéissent à des conditions de résonance.