






À la surface de l'eau, une onde progressive s'approche d'une paroi munie d'une double fente. Derrière la paroi, on observe un phénomène d'interférence. On observe qu'en menant une ligne parallèle à la paroi, les maximas et minimas y alternent régulièrement.

Un faisceau de lumière provenant d'un laser est élargi au moyen d'une baguette de verre, puis projeté sur une paroi munie d'une double fente. Un écran placé derrière la paroi fait apparaître des bandes alternativement claires et sombres: C'est un phénomène d'interférence semblable à celui qui a été décrit en haut.

La lumière est un phénomène ondulatoire
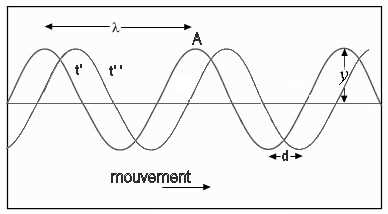
L'onde représentée se déplace de gauche à droite. Elle est représentée aux temps t' et t'' avec t''>t'. Pendant le temps t=t''-t', elle a parcouru la distance d. On définit:
Vitesse de l'onde (unité: $1\frac{m}{s}$): $v$ $=$ $\frac{d}{t}\;(1)$ Longueur d'onde (unité: $1\; m$): $\lambda$ = distance qui sépare deux sommets consécutifs en un temps donné
Un observateur situé en A voit défiler le sommet de l'onde. Après un temps $T$, il voit défiler le sommet suivant. L'onde a alors parcouru la distance $\lambda$. On définit:
Période de l'onde (unité: $1 \;s$): $T$ = temps que met un point de l'onde pour parcourir la distance $\lambda$
En employant (1), on obtient la relation fondamentale:
Relation fondamentale: $v$ $=$ $\frac{\lambda}{T}\;(2)$
Un observateur situé en A voit défiler $\nu$ sommets de l'onde en une seconde, c'est à dire que l'intervalle de temps $T$ est compris $\nu$ fois dans une seconde. On définit:
Fréquence de l'onde (unité: 1 Hertz = $1 Hz$ = $1\; s^{-1})$: $\nu$ $=$ $\frac{1}{T}\;(3)$
$\nu$ est donc le nombre de fois qu'un point de l'onde parcourt la distance $\lambda$ en une seconde. En employant (2) et (3), on reformule relation fondamentale:
$v$ $=$ $\lambda \nu\;(4)$