





Un corps se déplace de A vers B sous l'influence d'une force F qui fait un angle α avec la trajectoire. La force effectue un travail $W$
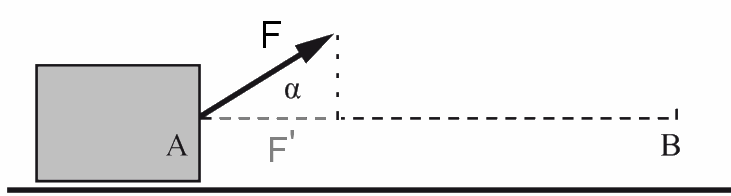
W = (projection de F sur AB) · AB W = F' · AB
Force faisant un angle $\alpha$ avec le déplacement: $W$ $=$ $F \cdot AB \cdot cos\alpha$
1 Joule = 1 Newton · 1 mètre $1\; J$ $ =$ $1\;N\cdot m$

$W$ $ =$ $F\cdot AB \cdot cos0^o$
Force parallèle au déplacement et de même sens: $W$ $=$ $F\cdot AB$

$W$ $=$ $F\cdot$ AB $\cdot cos180^o$
Force parallèle au déplacement et de sens opposé: $W$ $=$ $-F\cdot AB$

$W$ $=$ $F\cdot$ AB $\cdot cos90^o$
Force perpendiculaire au déplacement: $W$ $=$ $0$

- Un skieur de poids $650\; N$ dévale d'une montagne sur une piste de $2000\;m$ qui fait un angle de $60\;^o$ avec la verticale. Calculer le travail de son poids. Réponse: $W_P$ $=$ $650 \cdot 2000 \cdot cos 60\;^o$ $=$ $650000 \;J $

- Un skieur de poids $650\; N$ utilise un remonte-pente qui fait un angle de $110\;^o$ avec la verticale sur une longueur de $2000\;m$. Calculer le travail de son poids. $W_P$ $=$ $650 \cdot 2000 \cdot cos 110\;^o$ $=$ $-444626 \;J $