La chaleur est ce qui produit deux effets majeurs pour la matière qui la reçoit ou la perd : - une variation de température, ou - une variation de l'état physique (solide, liquide, gazeux) de la matière.
La "conduction" est le transport de chaleur qui se propage dans la matière à l'état solide, les métaux possédant une meilleure conductivité que les non-métaux. (Exemple: la cuiller métallique dans le café chaud)
Le "rayonnement thermique" est un transport de chaleur par les rayons infrarouges. (Domaine du spectre électromagnétique correspondant à des rayonnements de longueurs d'onde supérieures à celles de la lumière visible et inférieures à celles des micro-ondes). Tous les corps, pourvu qu'ils aient une température non nulle, émettent un rayonnement thermique. (Exemple: un poêle)
La chaleur provoque le déplacement des molécules au sein d'un liquide en général du bas vers le haut parce que le liquide chaud est moins dense que le liquide froid. (Exemple: le chauffage central à eau chaude)
Il faut deux fois plus de chaleur pour avoir une augmentation de température double:
La quantité de chaleur est proportionnelle à l'élevation de température.
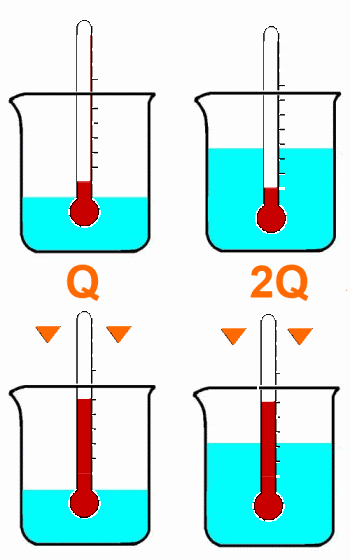Il faut deux fois plus de chaleur pour chauffer une masse double:
La quantité de chaleur est proportionnelle à la masse.
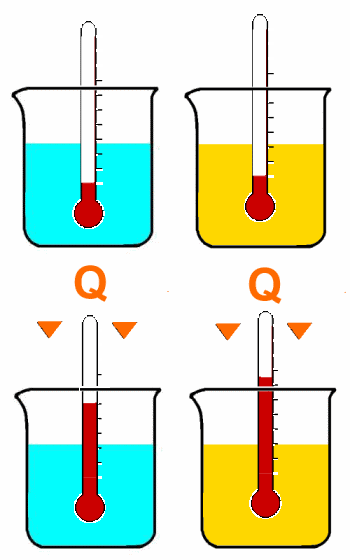Pour chauffer des matières différentes, on obtient un effet différent avec la même quantité de chaleur:
La quantité de chaleur dépend de la matière.
$\Delta Q$ $ =$ $ c\;m\;\Delta T$ avec: $\Delta Q$ : chaleur reçue $\Delta T$ : variation de température $m$ : masse $c$ : capacité calorifique (une constante qui dépend de la matière)
La calorie est la quantité de chaleur nécessaire pour élever la température d'un gramme d'eau de $1\;^oC$
En introduisant cette définition dans la formule fondamentale, il vient: $\Delta Q$ $ =$ $ c\;m\;\Delta T$ $1\;cal$ $=$ $c\cdot 1\;g\cdot 1\;K$ $c$ $=$ $\frac{1\;cal }{1g\;1K}$ $c$ $=$ $1 \frac{cal}{g \cdot K}$
Capacité calorifique de l'eau: $c_{_{H_2O}}$ $=$ $1 \;\frac{cal}{g \cdot K}$
Un dé de sucre a une masse de 3 g. La combustion d'un gramme de sucre libère $4\;kcal$. Combien de dés faut-il théoriquement brûler pour chauffer $600\;g$ de café (même $c$ que l'eau) de $20\;^oC$ à $100\;^oC$ ? Réponse: $\Delta Q$ $=$ $c\cdot m\Delta T $ $\Delta Q$ $=$ $1\cdot 600 \cdot (100-20)$ $=$ $48000\; cal$ $ =$ $48\; kcal$ Il faut donc brûler $\frac{48}{4}$ $=$ $12\;g$ de sucre soit $4$ morceaux!
