On appelle énergie d'une liaison chimique (enthalpie de dissociation d'une liaison), la variation d'enthalpie de la réaction qui dissocie une mole de telles liaisons.
Exemple:
À $25\;^oC$ et 1bar il faut fournir $436\;kJ$ de chaleur à une mole du gaz dihydrogène pour le dissocier entièrement en deux moles d'atomes d'hydrogène : $H_2(g)$ $\longrightarrow$ $2H(g)$ $\Delta H = +436\;kJ$ L'énergie de la liaison H-H (=l'enthalpie de la réaction de dissociation de $H_2$) = $436\;kJ$ !!
On trouve souvent le même type de liaison dans de nombreuses molécules, par exemple la liaison $C-H$ se trouve dans les molécules $CH_4$, $C_2H_6$, $C_{10}H_{22}$ etc... Comme son entourage est chaque fois légèrement différent, l'enthalpie de dissociation est légèrement différente. Dans le → Tableau des énergies de liaison on fait figurer une moyenne des valeurs différentes couramment rencontrées.
Les énergies de beaucoup de liaisons ont été déterminées. Elles permettent de prévoir approximativement les "chaleurs des réactions " à condition de connaître les liaisons des réactifs et produits}. Calculons approximativement la chaleur de la réaction : $2H_2O(g)$ $+$ $2Cl_2(g)$ $\longrightarrow$ $4HCl(g)$ $+$ $O_2(g)$
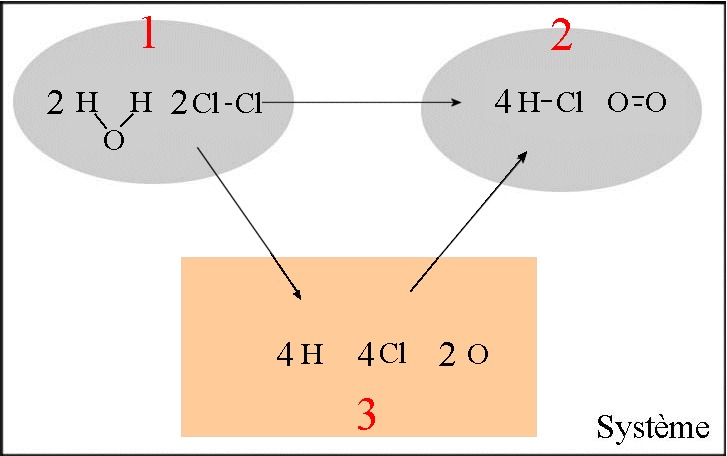
- Dans le cadre orange se trouvent les atomes isolés - Les transformations $1\rightarrow 3$ et $2\rightarrow 3$ sont des réactions de dissociation de liaisons chimiques ! $\Delta H_{12}$ $=$ $\Delta H_{13}$ $+$ $\Delta H_{32} =$ $\Delta H_{13}$ $-$ $\Delta H_{23} =$ $(4\cdot E_{liaison}(H-O)$ $ + $ $2\cdot E_{liaison}(Cl-Cl))$ $ - $ $(4\cdot E_{liaison}(H-Cl)$ $+$ $E_{liaison}(O=O))$ $ =$ $4\cdot 465$ $+$ $2\cdot 243$ $ -$ $(4\cdot 431$ $ +$ $494)$ $ =$ $128\;kJ$
Remarquez le résultat, légèrement différent de celui, plus correct, trouvé pour la même réaction avec les enthalpies de formation $(114,4\; kJ)$!
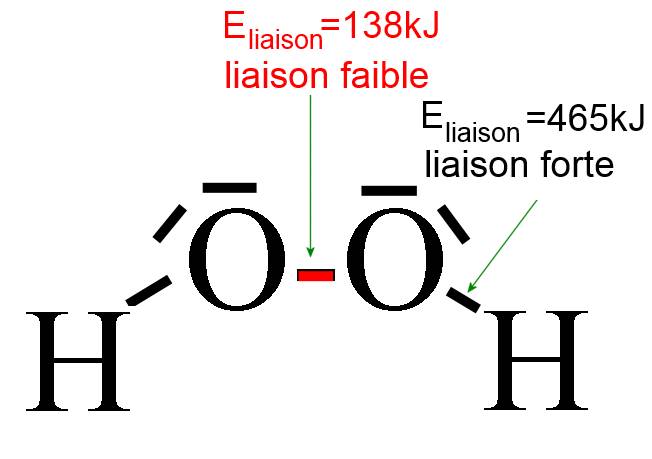
L'énergie de liaison est une bonne mesure pour évaluer la "force" des liaisons ( = la résistance à la rupture), par exemple dans la molécule d'eau oxygénée où la liaison O-O est fragile: