







On appelle réaction de formation d'une substance, la réaction chimique qui produit une mole de cette substance à partir des corps simples courants.
Exemple:
$H_2+\frac{1}{2}O_2$ $\longrightarrow$ $H_2O$ est la réaction de formation de l'eau, mais pas: $2H_2+O_2$ $\longrightarrow$ $2H_2O$ , en effet: - $H_2$ et $O_2$ sont bien les corps simples courants des éléments hydrogène et oxygène. - par contre, il est bien spécifié dans la définition qu'on doit considérer la réaction qui forme une mole de la substance en question!
On appelle enthalpie de formation d'une substance, la variation d'enthalpie de sa réaction de formation .
Exemple:
À $25^oC$ et 1bar la réaction de 2 mol du gaz (di)hydrogène avec une mole du gaz (di)oxygène pour produire 2 mol d'eau liquide dégage $571,66\; kJ$ : $2H_2(g)$ $+$ $O_2(g)$ $\longrightarrow$ $2H_2O(l)$ $\Delta H$ $=$ $- 571,66 kJ$ L'enthalpie de formation de l'eau = $\Delta H_f(H_2O)$ $=$ $\frac{571,66}{2}$ $=$ $- 285,83\;kJ$ !!
Les enthalpies de formation des espèces chimiques courantes ont été déterminées. Voir le → Tableau Elles permettent de prévoir toutes les "chaleurs des réactions " ( = -$\Delta H_{r\acute{e}action}$) et les "chaleurs des transformations"} ( = -$\Delta H_{transformation}$):
Exemple 1:
$2H_2O(g)+2Cl_2(g)$ $\longrightarrow$ $4HCl(g)+O_2(g)$
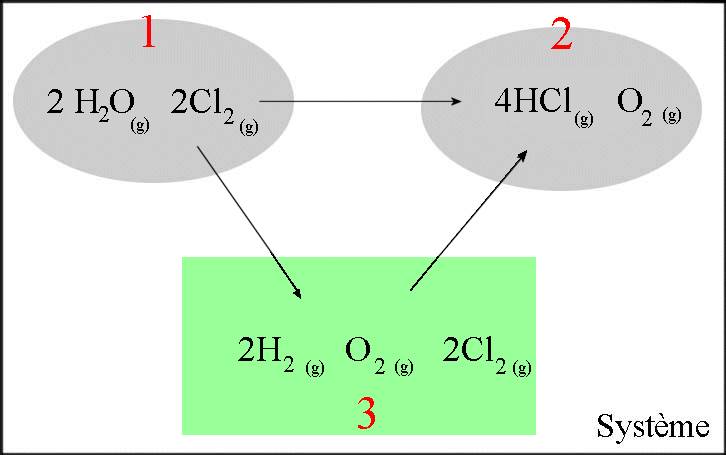
- Dans le cadre vert se trouvent les corps simples en question dans leur état normal - Les transformations $3\rightarrow 1$ et $3\rightarrow 2$ sont constituées de réactions de formation !
$\Delta H_{12}$ $=$ $\Delta H_{13}$ $+$ $\Delta H_{32}$ $=$ $\Delta H_{32}$ $-$ $\Delta H_{31}$ $=$ ($4\Delta H_f(HCl(g))$ $ +$ $\Delta H_f(O_2(g)))$ $-$ $(2\Delta H_f(H_2O(g))$ $+$ $2\Delta H_f (Cl_2(g)))$ $ =$ $(-4\cdot92,31$ $+$ $0)$ $ -$ $(-2\cdot 241,82$ $+$ $2\cdot 0)$ $=$ $114,4\;kJ$
La variation d'enthalpie de cette réaction, effectuée dans les proportions stoechiométriques à $298\;K$ et $1\;bar$ vaut $114,4\;kJ$. La réaction, effectuée dans les proportions stoechiométriques à $298\;K$ et $1\;bar$ absorbe donc $114,4\;kJ$ de chaleur. La "chaleur de réaction", effectuée dans les proportions stoechiométriques à $298\;K$ et $1\;bar$ vaut $-114,4\;kJ$.
Notons une propriété utile rencontrée dans cet exemple :
Lors d'une réaction chimique: $\Delta H(r\acute{e}action)$ $=$ $\Sigma \Delta H_f(produits)$ $-$ $\Sigma \Delta H_f(r\acute{e}actifs)$ ($\Sigma$ = Somme)
Exemple 2:
$2H_2O(g)$ $\longrightarrow$ $2H_2O(l)$
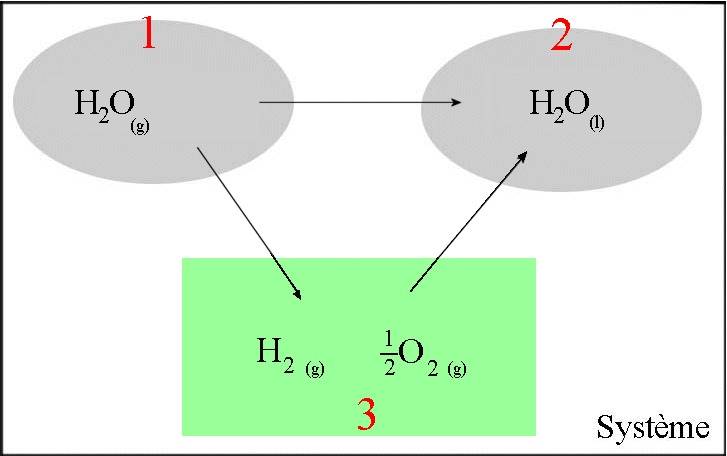
- Dans le cadre vert se trouvent les corps simples en question dans leur état normal. - Les transformations $3$ $\rightarrow$ $1$ et $3$ $\rightarrow$ $2$ sont constituées de réactions de formation !
$\Delta H_{12} =$ $\Delta H_{13}$ $+$ $\Delta H_{32} =$ $\Delta H_{32}$ $-$ $\Delta H_{31} =$ $\Delta H_f(H_2O(l))$ $-$ $\Delta H_f(H_2O(g)) =$ $-285,83$ $-$ $(-241,82) =$ $-44,01\;kJ$
La variation d'enthalpie de cette réaction, effectuée dans les proportions stoechiométriques à $298\;K$ et $1\;bar$ vaut $-44,01\;kJ$. La transformation d'une mole de vapeur d'eau en eau liquide, effectuée à $298\;K$ et $1\;bar$ libère donc $44,01\;kJ$ de chaleur. La chaleur de condensation, à $298\;K$ et $1bar$ vaut $44,01\;kJ$.
Notons encore une propriété utile rencontrée dans cet exemple :
Lors d'une transformation physique d'une substance: $\Delta H$(transformation physique) =$\Delta H_f$ (substance à l'état final)- $\Delta H_f$(substance à l'état initial)