





Un système matériel (p.ex. un téléphérique en mouvement) peut posséder globalement de l'énergie cinétique du fait de sa vitesse et de l'énergie potentielle (du fait de sa hauteur ou de la tension du cable ou de la charge d'une batterie) En chimie nous nous intéressons cependant à des systèmes constitués d'un ensemble de substances à l'intérieur du récipient où elles réagissent. Les facteurs globaux tels la vitesse avec laquelle se déplace le récipient ou la hauteur où il se trouve n'ont aucun intérêt pour caractériser ces systèmes chimiques.
Le système formé par 2 moles $H_2$ et 1 mole $O_2$ n.t.p. peut fournir dans cet état beaucoup plus de travail au milieu extérieur que dans l'état où il s'est transformé en deux moles d'eau. (la preuve: moteur à hydrogène!). Il doit donc exister des facteurs qui déterminent l'énergie interne du système.
L'énergie interne $U$ d'un système chimique en un moment donné vient en réalité - de l'énergie cinétique de toutes les espèces chimiques, molécules, atomes ou ions qui constituent ce système - de l'énergie potentielle renfermée dans les liaisons chimiques. Considérez ces liaisons comme des ressorts, dans certains cas plus "tendus" que dans d'autres, donc possédant plus d'énergie!

Mouvement des molécules de l'eau
Il est beaucoup trop compliqué d'évaluer l'énergie interne U en considérant individuellement les mouvements et interactions du nombre énorme d'espèces qui constituent les systèmes chimiques! Mais en principe l'énergie interne U doit pouvoir être calculée à partir des paramètres d'état $P,V,T$ et $n_i$. (On dit que U est fonction d'état). Comme même ce calcul s'est révélé trop compliqué dans beaucoup des cas concrets, on étudie plutôt les variations de U quand un système passe d'un état à un autre. En effet, toute réaction chimique complète peut être considérée comme le passage d'un système d'un état initial (les réactifs) à un état final (les produits).
La physique nous enseigne que chaleur et travail sont deux formes d'énergie "équivalentes", c'est-à-dire qu'elles peuvent être transformées l'une dans l'autre . Voilà pourquoi elles s'expriment dans la même unité: 1 Joule($J$) = 1 Newton $\cdot$ mètre ($Nm$)
L'énergie se conserve globalement
Appliquons cette loi fondamentales aux systèmes chimiques: Si un système gagne de l'énergie (donc si son énergie interne augmente), cette énergie doit provenir du milieu extérieur sous forme de chaleur et (ou) travail . En désignant par $Q$ et $W$ les chaleur et travail reçues par le système, on a:
$\Delta U$ $ = $ $Q$ $+$ $W$
Rappelez-vous que $\Delta U$ signifie $U_{final}$ $-$ $U_{initial}$ donc désigne le gain d'énergie interne. (Si $\Delta U <0$, la même équation signifie que l'énergie interne diminuant, cette l'énergie perdue doit se retrouver au milieu extérieur sous forme de chaleur et (ou) travail).
La chaleur et le travail échangés par un système chimique avec le milieu extérieur sont faciles à mesurer, donc nous pouvons déterminer expérimentalement la variation de l'énergie interne pendant une transformation chimique!
Le travail échangé entre un système chimique et le milieu extérieur provient dans la plupart des cas uniquement des variations de volume. Dans le moteur à explosion d'une automobile, l'explosion des gaz (= le système) fournit du travail au piston et fait avancer la voiture (= le milieu extérieur).
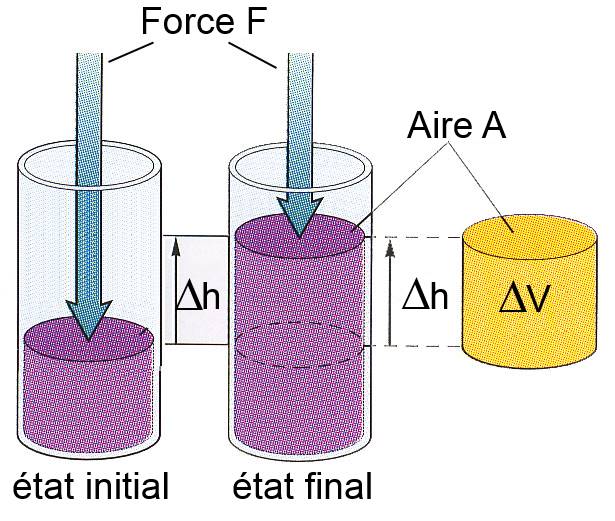
Dans la plupart des applications chimiques, les réactions se font à pression constante (souvent la presion atmosphérique): Appelons cette pression $P$. Comme la pression est définie comme $P$ $=$ $\frac{F}{A}$, le gaz (système) représenté se détend donc contre la force constante $F$ $=$ $P\cdot A$ et fournit au milieu extérieur le travail: $F\cdot\Delta h$ $=$ $P\cdot\Delta h\cdot A$ $=$ $P\cdot\Delta V$
Travail reçu par le système: $W$ $ =$ $-P\cdot\Delta V$
Les mesures des quantités de chaleur échangées avec le milieu extérieur se font dans le calorimètre:
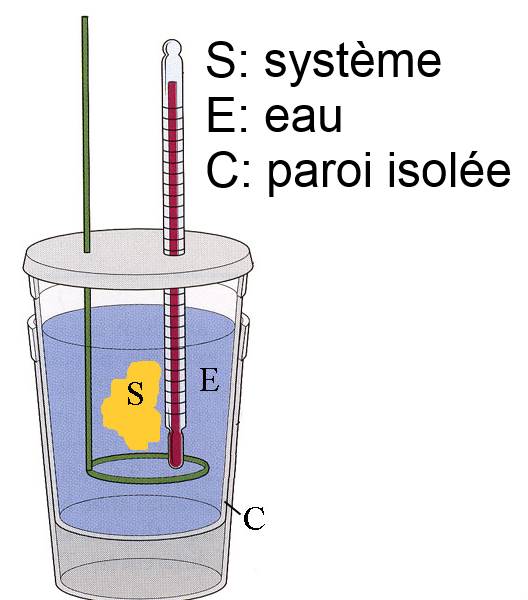
S : Le système formé par les espèces chimiques qui réagissent et leurs produits E : L'eau fait partie du milieu extérieur, elle reçoit une quantité de chaleur (en Joule) égale à $4184 \cdot m \cdot (\theta_f$ $-$ $\theta_i)$ où $4184 \frac{J}{kg \cdot K}$ est la capacité thermique massique de l'eau (= nombre de Joules nécessaires pour élever la température d'un kilogramme d'eau de 1K) $m$ la masse de l'eau (en kilogrammes), $\theta_i$ la température au début de la réaction et $\theta_f$ la température en fin de réaction (voir physique) C : Le calorimètre fait partie du milieu extérieur, il reçoit une quantité de chaleur (en Joule) égale à $C\cdot (\theta_f$ $-$ $\theta_i)$ où $C$ est sa capacité thermique (en Joules par degré)
Chaleur reçue par le système: $Q$ $=$ $-4184 \cdot m \cdot (\theta_f$ $-$ $\theta_i)$ $-$ $C\cdot (\theta_f$ $-$ $\theta_i)$ où: $Q$ (en Joule) est la quantité de chaleur reçue par le système, $m$ (en kilogrammes) la masse de l'eau, $C$ (en Joule par degré) la capacité thermique du calorimètre $\theta_i,\theta_f$ sont les températures initiale repectivement finale,
0,625 g de formaldéhyde ($H_2CO$) sont par exemple brûlées dans un calorimètre ouvert: $H_2CO$ $+$ $O_2$ $\longrightarrow$ $CO_2$ $+$ $H_2O$ La température du bain d'eau ($150 g\; H_20$) s'élève de $24,0\; ^oC$ à $39,2\; ^oC$. La capacité thermique du calorimètre vaut $150 \frac{J}{K}$: $Q$ $=$ $-4184 \cdot 0,150 \cdot 15,2$ $-$ $150 \cdot 15,2$ $ \approx$ $-11820 J$
La calorie est une ancienne unité pour la quantité de chaleur:
Une calorie (1 cal) est la quantité de chaleur nécessaire pour élever la température de 1 gramme d'eau de 1 degré
En portant dans l'équation (2) où nous laissons le deuxième terme de côté, nous trouvons: $1 cal$ $=$ $4184\cdot 0,001\cdot 1$ $=$ $4,184 J$
$1\; cal$ $=$ $4,184\; J$ $1\; Joule$ $=$ $0,239 \;cal$
Les chimistes préfèrent (encore) souvent prendre la calorie pour unité de la quantité de chaleur et le gramme pour unité de la masse. L'équation (3) devient dans ce cas:
Chaleur reçue par le système: $Q$ $=$ $- 1\cdot m \cdot (\theta_f$ $-$ $\theta_i)$ $-$ $C\cdot (\theta_f$ $-$ $\theta_i)$ où: $1\frac{cal}{g\cdot K}$ est la capacité thermique massique de l'eau, $Q$ est exprimée en $cal$, $m$ en g $C$ en $\frac{cal}{K}$
Si nous nous arrangeons pour que le travail $W$ reçu par le système s'annulle dans l'équation (2): $\Delta U$ $=$ $Q$ , la variation d'énergie interne sera simplement la chaleur reçue par le système qu'on pourra déterminer par calorimètrie!! Pour cela, il faut éviter les changements de volume qui sont seuls responsables du travail échangé par le système en chimie, c'est-à-dire qu'il faut opérer à volume constant dans un calorimètre hermétiquement clos ("=bombe calorimétrique"):

Dans un calorimètre fermé (à volume constant): Variation de l'énergie interne du système: $\Delta U$ $=$ $Q$ = Chaleur reçue par le système