Voici une solution $0,200 M$ de $H_3C_6H_5O_7$ (acide citrique, $K_a$ $=$ $3,5 \cdot 10^{-4}$)
Equilibre d'hydrolyse:
$H_3C_6H_5O_7$ $+$ $H_2O$
$H_3O^+$ $+$ $H_2C_6H_5O_7^-$
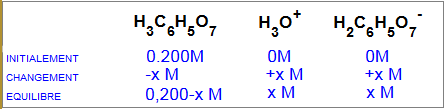
$K_a$ $ = $ $3.5 \cdot 10^{-4}$ $ = $ $\frac{x^2 }{ 0,200-x}$
En résolvant, nous trouvons $x$ $=$ $8,4\cdot 10^{-3}\;M $ $=$ $[H_3O^+]$. Quelle est l'étape finale pour calculer le $pH$ de cette solution?
a) trouver le $pH$ par la formule $pH$ $=$ $- log (K_a)$ b) trouver le $K_a$ en substituant cette valeur de $[H_3O^+]$ dans l'expression de $K_a$ c) trouver le $pH$ par la formule $pH$ $ =$ $- log [H_3O^+]$ $=$ $-log x$
La réponse c) est correcte, $pH$ $=$ $-log x$ $=$ $2,08$