On trouve l'élément fer sous trois états:
Le fer métal, symbole: $Fe$, ici sous forme de clous.
L'ion fer(II), symbole: $Fe^{2+}$, ici par exemple dans lasubstance ionique sulfate de fer(II).
L'ion fer(III), symbole: $Fe^{3+}$, ici par exemple dans la substance ionique chlorure de fer(III)
Dans l'ion fer(III) , l'élément fer est plus oxydé (a perdu plus d'électrons!) que dans le fer(II) où il est encore plus oxydé que dans le fer métal:
On caractérise le dégré d'oxydation par un nombre appelé le nombre d'oxydation (n.o.)
n.o.($Fe^{3+}$)=3 n.o.($Fe^{2+}$)$ $=$ $2 n.o.($Fe$)$ $=$ $0
Nombre d'oxydation d'un atome neutre = 0 Nombre d'oxydation d'un ion monoatomique = sa charge
n.o.($Cl^{-}$)=-1 n.o.($S^{2-}$)$ $=$ $-2 n.o.($Al^{3+}$)$ $=$ $3 n.o.($Mg$)$ $=$ $0
Cette définition est élargie aux ions composés et aux molécules:
Nombre d'oxydation d'une molécule (neutre)= 0 Nombre d'oxydation d'un ion polyatomique = sa charge
n.o.($Cl_2$)=0 n.o.($SO_4^{2-}$)$ $=$ $-2 n.o.($NH_4^{+}$)$ $=$ $1 n.o.($H_2O_2$)$ $=$ $0
Il s'avère utile de définir un nombre d'oxydation pour chaque atome à l'intérieur d'un ion composé ou d'une molécule. On estime alors grossièrement que l'espèce se trouve dissociée enièrement en ions:
Pour chaque liaison, on attribue tous les électrons de cette liaison à l'atome le plus électronégatif. Si les atomes ont même électronégativité, on attribue à chaque atome un électron de la liaison. La charge résultante de l'atome détermine son nombre d'oxydation.
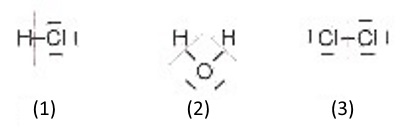
(1) On attribue les 2 électrons de la liaison au chlore qui possède ainsi 8 électrons dans sa dernière couche (1 de plus que la structure de Lewis de l'atome neutre) Il restera à l'atome d'hydrogène 0 électrons dans sa dernière couche (1 de moins que la structure de Lewis de l'atome neutre): n.o.($H$ dans $HCl$ $=$ $1$) n.o.($Cl$ dans $HCl$ $=$ $-1$) (2)On attribue les 4 électrons des deux liaisons à l'oxygène qui possède ainsi 8 électrons dans sa dernière couche (2 de plus que la structure de Lewis de l'atome neutre); Il restera à chaque atome d'hydrogène 0 électrons dans sa dernière couche (1 de moins que la structure de Lewis de l'atome neutre): n.o.($H$ dans $H_2O$ $=$ $1$) n.o.($O$ dans $H_2O$ $=$ $-2$ (3) On attribue un électron de la liaison à chaque atome de chlore qui possède ainsi 7 électrons dans sa dernière couche (autant que la structure de Lewis de l'atome neutre) n.o.($Cl$ dans $Cl_2$) = 0
Des exemples précédents se dégagent les règles pratiques suivantes:
N.o. de $H$ dans une espèce (ion ou molécule) composée= 1 N.o. de $O$ dans une espèce (ion ou molécule) composée = -2 N.o. de $F,Cl,Br,I,$ dans une espèce (ion ou molécule) composée = -1
La première règle s'applique évidemment seulement, si $H$ est le moins électronégatif, la 2e et 3e si $O,F,Cl,Br,I$ sont les plus électronégatifs dans les liaisons qu'ils forment. n.o.($H$) dans $C_2H_6$ $=$ $1$ n.o.($H$) dans $H_2$ $=$ $0$ n.o.($Cl$) dans $ClBr$ $=$ $-1$ n.o.($Br$) dans $ClBr$=+1 !
On remarque encore: n.o.($H_2O$)=0 =$2\cdot$n.o.($H$ dans $H_2O$)+n.o.($O$ dans $H_2O$) n.o.($OH^{-}$)$ $=$ $-1$ = $n.o.($O$ dans $OH^-$)+n.o.($H$ dans $OH^-$)
Somme des n.o. des atomes dans une molécule}= 0 Somme des n.o. dans un ion composé = sa charge
Toutes ces règles pratiques permettent la détermination des n.o. par simple calcul algébrique, par exemple: Calculer le n.o.(S dans $SO_2$) Appelons le n.o. cherché $x$: $x$ $+$ $2(-2)$ $=$ $0$ $x$ $=$ $4$ En effet: Le n.o.(O)dans le corps composé est -2 et la somme des n.o. de la molécule vaut 0 Calculer le n.o.(N dans $NO_3^-$) Appelons le n.o. cherché $x$: $x$ $+$ $3(-2)$ $=$ $-1$ $x$ $=$ $5$ En effet: Le n.o.(O)dans le corps composé est -2 et la somme des n.o. de l'ion $NO_3^-$ vaut -1
Exemple: Nombres d'oxydation dans la synthèse du bromure d'aluminum:
| $Al$ | $-3e^-$$\longrightarrow $ | $ Al^{3+}$ | (1) | $0$ | $3$ | $Br_2$ | $+2e^-$$\longrightarrow $ | $2 Br^{-}$ | (2) | $2\cdot 0$ | $2\cdot -1$ |
Si le nombre d'oxydation diminue de n unités alors le corps gagne n électrons Si le nombre d'oxydation augmente de n unités alors le corps perd n électrons
..ce qui n'est que logique, puisque nous avons assimilé le nombre d'oxydation à une charge fictive!
Exemple: Nombres d'oxydation dans la réduction de l'ion peroxodisulfate:
| $S_2$$O_8^{2-}$ | $......$$\longrightarrow $ | $2S$$O_4^{2-}$ | (1) | $2\cdot7$ | $2\cdot6$ |