Recherche:
Ce sont des réseaux où ions positifs A et ions négatifs B sont en nombre égal.
La taille respective des ions détermine le type de réseau:
Si les ions positifs et négatifs ont approximativement la même taille, on trouve souvent le réseau du type
chlorure de césium $Cs^+Cl^-$)
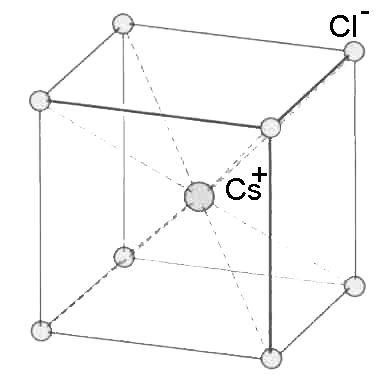- Si le diamètre des ions positifs est environ la moitié de celui des ions négatifs, on trouve souvent le réseau du type
Chlorure de sodium $Na^+Cl^-$
- Si le diamètre des ions positifs est environ le quart de celui des ions négatifs, on trouve souvent le réseau du type
Blende $Zn^{2+}S^{2-}$,
(sulfure de zinc)
Ce sont des réseaux où on trouve deux fois plus d'ions négatifs B que d'ions positifs A.
La taille respectives des ions détermine le type de réseau:
- Si les ions positifs et négatifs ont approximativement la même taille, on trouve souvent le réseau du type
Fluorite $Ca^{2+}(F^-)_2$,
(fluorure de calcium)
- Si le diamètre des ions positifs est environ la moitié de celui des ions négatifs, on trouve souvent le réseau du type
Rutile $Ti^{4+}(O^{2-})_2$,
(oxyde de titane(IV))
La maille élémentaire est le plus petit volume découpé dans un réseau qui reproduit le réseau entier quand il est juxtaposé à lui-même dans tous les sens.
La maille renferme $1$ cation (au centre) et $8\cdot \frac{1}{8}$ $=$ $1$ anion.
Les ions se touchent uniquement sur la diagonale $d$ et non sur l'arête $a$.
On a:
$d$ = diamètre de l'anion + diamètre du cation
$d$ $=$ $a\sqrt{3}$
Volume de la maille =
$V$ $=$ $a^3$
La maille renferme $1$ cation (au centre), $6\cdot \frac{1}{2}$ $=$ $3$ anions aux milieux des faces, $8\cdot \frac{1}{8}$ $=$ $1$ anion sur les sommets et $12\cdot \frac{1}{4}$ $=$ $3$ cations aux milieux des arêtes. Les ions se touchent uniquement sur l'arête $a$ et non sur la diagonale $d$. On a: $a$ = diamètre de l'anion + diamètre du cation $d$ $=$ $a\sqrt{3}$ Volume de la maille = $V$ $=$ $a^3$
La maille élémentaire détermine souvent la structure cristalline des solides, mais pas toujours. La cristallographie étudie la géométrie des systèmes cristallins.