





Un équilibre hétérogène est un équilibre chimique entre substances intervenant dans des phases différentes dont au moins une de ces substances se trouve dans une phase où sa concentration est constante.
Supposons par exemple que le réactif $Y$ se trouve en phase solide , le réactif $X$ et les produits $C$ et $D$ en phase gazeuse: $aX_{(g)}$ $+$ $b$ $Y_{(s)}$$ \leftrightarrows$ $cC_{(g)}$ $+$ $dD_{(g)} $ (1) On peut considérer que la réaction n'est possible que si $Y$ est d'abord extrait de la phase solide pour passer en phase gazeuse: $Y_{(s)}$$\leftrightarrows$$Y_{(g)}$ (2) Nous sommes en présence d'un équilibre hommogène (1) et d'un équilibre hétérogène (2):
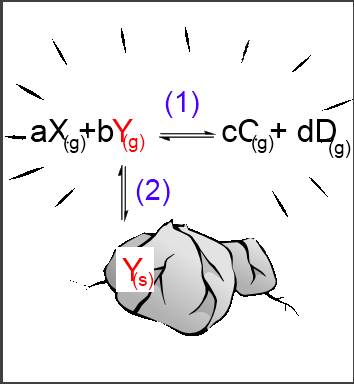
Appliquons les lois d'équilibre pour ces deux cas (1):$\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a\cdot[Y_{(g)}]^b}$ $=$ $K_c $ (2):$[Y_{(g)}]$ $=$ $K_{sat} $ (2) dans (1) : $\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a\cdot K_{sat}^b}$ $=$ $K_c $ $\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a}$ $=$ $K_c\cdot K_{sat}^b $ $ K_c\cdot K_{sat}^b$ est une nouvelle constante que nous désignerons par $K$, d'où:
Pour un équilibre hétérogène $aX_{(g)}+b$ $Y_{(s)}$$ \leftrightarrows$ $cC_{(g)}$ $+$ $dD_{(g)} $, on a: $\frac{[C_{(g)}]^c\cdot[D_{(g)}]^d}{[X_{(g)}]^a}$ $=$ $K $ Dans la loi de Gulberg et Waage, on peut laisser de côté l'espèce chimique intervenant dans la phase où sa concentration est constante!