






Dans cette expérience la couleur (donc la concentration !) d'un réactif diminue avec le temps. En physique, on définit la vitesse d'un mobile comme le rapport entre la distance parcourue ( = variation de la distance) et le temps nécessaire pour parcourir cette distance ( = variation du temps). Par analogie, en chimie, il vient l'idée de définir la vitesse d'une réaction comme le rapport entre la variation de concentration et le durée de cette variation ( = variation du temps).
Si $\Delta [X]$ est la variation de la molarité d'un réactif X ( = molarité finale - molarité initiale!), grandeur négative (la molarité du réactif X diminue!), et $\Delta t$ la durée de cette variation, alors on définit:
Vitesse d'une réaction chimique par rapport à un réactif X : $v_X$ $=$ $\frac{\Delta[X]}{\Delta t}$
( Le signe - vient du fait qu'on voudrait avoir une vitesse positive!)
Si on définissait la vitesse par rapport un produit Y de la réaction, il faudrait évidemment laisser ce signe - de côté, puisqu'alors la molarité du produit augmenterait au cours du temps!
Vitesse d'une réaction chimique par rapport à un produit Y : $v_Y$ $=$ $\frac{\Delta[Y]}{\Delta t}$
La vitesse définie jusqu'ici est la vitesse moyenne de la réaction entre deux temps $t_i$ (temps initial) et $t_f$ (temps final) avec $\Delta t$ $=$ $t_f$ $-$ $t_i$.

Vitesse moyenne entre C et B = $-\frac{[X_f]-[X_i]}{t_f-t_i}$ = - pente de la sécante par C et B
(dans ce cas) = $-\frac{0,3-0,56}{60-20}$ = $0,0065$ $\frac{mol}{L\cdot s}$
Si on rend cette différence très petite, on obtient une vitesse "instantanée".
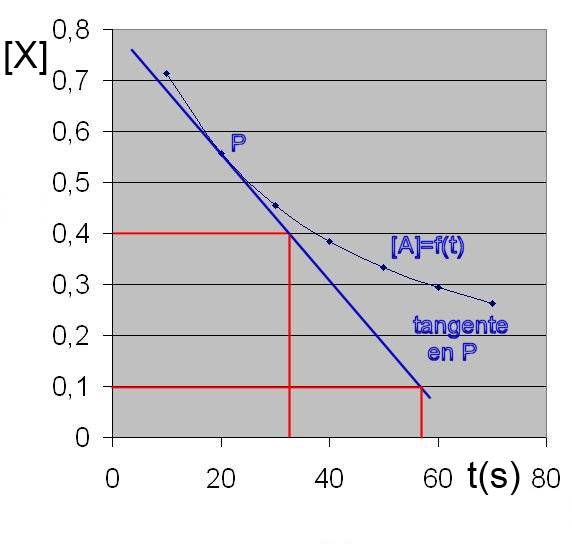
Vitesse instantanée en P = - pente de la tangente en P
(dans ce cas) = $-\frac{0,1-0,4}{56-32}$ = $0,0125$ $\frac{mol}{L\cdot s}$