





La vodka est un mélange d'alcool et d'eau.

L'eau est le solvant L'alcool est le soluté, (désormais noté: $so$) La vodka est la solution, (désormais notée: $S$)
La masse volumique de la solution est le rapport de la masse de la solution par son volume:
Masse volumique de la solution: $\rho_S$=$\frac{m_S}{V_S}$
Par exemple, $\rho_{S}$ $=$ $0,95\frac{g}{cm^{3}}$ veut dire que 1 $cm^3$ de la solution $S$ a une masse de $0,9 g$ En effet, dans ce cas, on a: $\rho_{S}$ $=$ $\frac{0,95}{1}$ $=$ $0,95\frac{g}{cm^{3}}$
Le nombre de moles du soluté est le rapport de la masse du soluté par sa masse molaire.
Nombre de moles du soluté: $n_{so}$ $=$ $\frac{m_{so}}{M_{so}}$
Par exemple $18 g$ de glucose $(C_6H_{12}O_6)$ sont $n_{glucose}$ $=$ $\frac{18}{6\cdot 12+12\cdot 1+ 6\cdot 16}$ $=$ $0,1 $ mol
Le pourcentage du soluté est le rapport de la masse du soluté par la masse de la solution, le tout multiplié par $100$
Pourcentage du soluté: $\%_{so}$ $=$ $\frac{m_{so}\cdot 100}{m_S}$
Par exemple, $\%_{so}$ $=$ $24$ veut dire que $100 g$ de la solution $S$ renferment $24 g$ du soluté $so$ En effet, dans ce cas, on a: $\%_{so}$=$\frac{24\cdot 100}{100}=24$
La molarité du soluté est le rapport du nombre de moles du soluté par le volume de la solution.
Molarité du soluté: $[so]$ $=$ $\frac{n_{so}}{V_S}$
Par exemple, $[so]$ $=$ $2\frac{mol}{L}$ $=$ $2M$ (ne pas confondre avec la masse molaire M!) veut dire que $1 L$ de la solution $S$ renferment 2 mol du soluté $so$ En effet, dans ce cas, on a: $[so]$ $=$ $\frac{2}{1}$ $=$ $2\frac{mol}{L}$
Chaque triangle coloré correspond à l'une des formules précédentes:
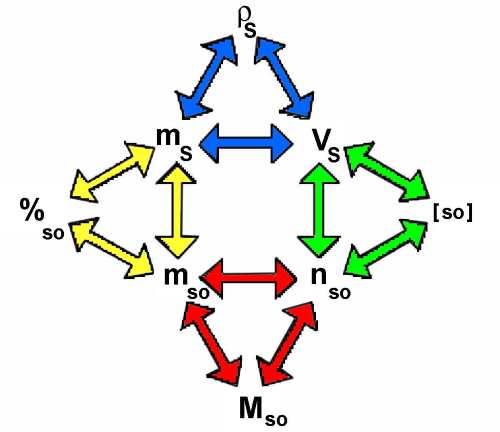
Dans chaque triangle, une grandeur peut être calculée, si on connaît les deux autres. Le schéma permet de passer d'un triangle à l'autre.
Exemple:
$3 \;L$ d'une solution de masse volumique $\rho_{S}$ $=$ $1,2\frac{g}{cm^3}$ renferment $2\; mol$ d'un soluté de masse molaire $M_{so}$ $=$ $72\frac{g}{mol}$. Calculer le pourcentage du soluté dans cette solution!
Réponse:
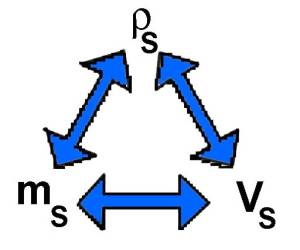
$3L$ $=$ $3000cm^3$ $\rho_S$=$\frac{m_S}{V_S}$ $ m_S$ $=$ $\rho_S\cdot V_S$ $m_S$ $=$ $1,2\cdot 3000$ $=$ $3600 g$
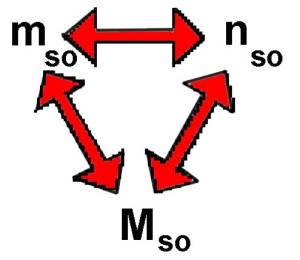
$n_{so}$ $=$ $\frac{m_{so}}{M_{so}}$ $m_{so}$ $=$ $n_{so}\cdot M_{so}$ $m_{so}$ $=$ $2\cdot 72$ $=$ $144 g$
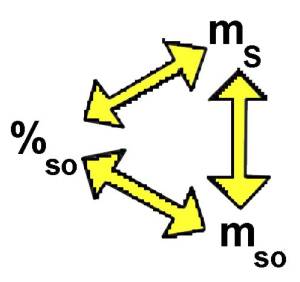
$\%_{so}$ $=$ $\frac{m_{so}\cdot 100}{m_S}$ $\%_{so}$ $=$ $\frac{144\cdot 100}{3600}$ $=$ $4$ La solution possède $4\%$ de soluté.